题目内容
 如图所示,某地一天从6时至14时的温度变化曲线近似满足y=Asin(ωx+φ)+b.
如图所示,某地一天从6时至14时的温度变化曲线近似满足y=Asin(ωx+φ)+b.(1)求这段时间的最大温差;
(2)写出这段曲线的函数解析式;
(3)如果一天24小时内的温度均近似符合该函数关系式,求一天中温度不小于25℃的时间有多长?
分析:(1)依题意,由图可知这段时间的最大温差为30°-10°=20°;
(2)由图得A=10,
T=8,从而可求得ω,又该曲线过点P(10,20),可求得φ,于是可得这段曲线的函数解析式;
(3)由10sin(
x+
)+20≥25⇒16k-
≤x≤
+16k(k∈Z),又6≤x≤14⇒
≤x≤14,于是可得答案.
(2)由图得A=10,
| 1 |
| 2 |
(3)由10sin(
| π |
| 8 |
| 3π |
| 4 |
| 14 |
| 3 |
| 2 |
| 3 |
| 34 |
| 3 |
解答:解:(1)由图知,这段时间的最大温差为30°-10°=20°;
(2)∵b=
=20,A=
=10,又
T=14-6=8,
∴T=16=
,
∴ω=
,
∴这段曲线的函数解析式为y=10sin(
x+φ)+20,
又该曲线过点P(10,20),
∴
×10+φ=2kπ(k∈Z),
∴φ=2kπ-
(k∈Z),不妨令k=1,得φ=
,
∴这段曲线的函数解析式为y=10sin(
x+
)+20(6≤x≤14);
(3)由10sin(
x+
)+20≥25得:sin(
x+
)≥
,
∴
+2kπ≤
x+
≤
+2kπ(k∈Z),
∴16k-
≤x≤
+16k(k∈Z),又6≤x≤14,
∴16-
≤x≤14,即
≤x≤14.
∴一天中温度不小于25℃的时间有14-
=
小时.
(2)∵b=
| 30+10 |
| 2 |
| 30-10 |
| 2 |
| 1 |
| 2 |
∴T=16=
| 2π |
| ω |
∴ω=
| π |
| 8 |
∴这段曲线的函数解析式为y=10sin(
| π |
| 8 |
又该曲线过点P(10,20),
∴
| π |
| 8 |
∴φ=2kπ-
| 5π |
| 4 |
| 3π |
| 4 |
∴这段曲线的函数解析式为y=10sin(
| π |
| 8 |
| 3π |
| 4 |
(3)由10sin(
| π |
| 8 |
| 3π |
| 4 |
| π |
| 8 |
| 3π |
| 4 |
| 1 |
| 2 |
∴
| π |
| 6 |
| π |
| 8 |
| 3π |
| 4 |
| 5π |
| 6 |
∴16k-
| 14 |
| 3 |
| 2 |
| 3 |
∴16-
| 14 |
| 3 |
| 34 |
| 3 |
∴一天中温度不小于25℃的时间有14-
| 34 |
| 3 |
| 8 |
| 3 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查实际应用问题,求得这段曲线的函数解析式是关键,也是难点,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
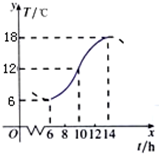 如图所示,某地一天从6~14时的温度变化曲线近似满足函数:f(x)=Asin(ωx+φ)+b,x∈[6,14],则这段曲线的解析式为( )
如图所示,某地一天从6~14时的温度变化曲线近似满足函数:f(x)=Asin(ωx+φ)+b,x∈[6,14],则这段曲线的解析式为( )A、f(x)=12sin(
| ||||
B、f(x)=6sin(
| ||||
C、f(x)=6sin(
| ||||
D、f(x)=12sin(
|
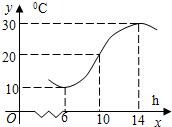 如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为
如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为

 如图所示,某地一天从6~14时的温度变化曲线近似满足函数:f(x)=Asin(ωx+φ)+b,x∈[6,14],则这段曲线的解析式为( )
如图所示,某地一天从6~14时的温度变化曲线近似满足函数:f(x)=Asin(ωx+φ)+b,x∈[6,14],则这段曲线的解析式为( )


