题目内容
(理)设数列{an}满足条件:a1=a(a>2),且an+1=(1)证明:an>2;
(2)证明:a1+a2+…+an<2(n+a-2);
(3)若xn=![]() ,求数列{xn}的通项公式
,求数列{xn}的通项公式
(文)已知数列{an}和{bn}满足:a1=![]() ,且an+bn=1,bn+1=
,且an+bn=1,bn+1=![]() (n∈N*).
(n∈N*).
(1)求数列{an}与{bn}的通项公式;
(2)设Sn=a1+a2+a2a3+…+anan+1.若对任意的n∈N*,不等式kSn>bn恒成立,求正整数k的最小值.
答案:(理)(1)①当n=1时,∵a1=a>2,∴命题an>2成立
②假设n=k时命题成立,那么有ak>2成立.
当n=k+1时,
∵ak+1-2=![]() >0,∴ak+1>2
>0,∴ak+1>2
即当n=k+1时命题成立.
综上所述,当n∈N*时,an>2成立.
(2)∵an+1=![]() ,∴an=
,∴an=![]() (n≥2)
(n≥2)
又∵an-2=![]()
∴an-2<![]() (n≥2).
(n≥2).
∴(a1-2)+(a2-2)+…+(an-2)
≤(a-2)(1+![]() )
)
=(a-2)![]()
=2(a-2)(1![]() )<2(a-2),
)<2(a-2),
∴a1+a2+…+an<2(n+a-2).
(3)解法一:∵an+1=![]() ,
,
∴![]() ,
,
即![]() ,
,
∵xn=![]() ,∴xn+1=2(xn
,∴xn+1=2(xn![]() )
)
即xn=2(xn-1![]() )(n≥2)
)(n≥2)
∴![]() -xn=2(
-xn=2(![]() -xn-1+
-xn-1+![]() )=2(
)=2(![]() -xn-1)2
-xn-1)2
∵![]() -xn=2(
-xn=2(![]() -xn-1)2=2[2(
-xn-1)2=2[2(![]() -xn-2)2]2
-xn-2)2]2
=21+2![]()
=…=![]()
=![]() ,
,
∴xn=![]()
解法二:∵(![]() )2=
)2=![]() (
(![]() -xn+1)
-xn+1)
设bn=![]() -xn,则b1=
-xn,则b1=![]() ,bn>0,bn+1=2
,bn>0,bn+1=2![]() ,
,
∴lgbn+1=lg2+2lgbn,
∴lgbn+1+lg2=2(1gbn+lg2),即lg2bn+1=2lg2bn
∴{lg2bn}是等比数列,公比q=2,
lg2b1=lg(1![]() ),
),
lg2bn=2n-1lg(1![]() )=lg(1
)=lg(1![]() )
)![]()
∴2bn=![]() ,即1-2xn=
,即1-2xn=![]() ,
,
∴xn=![]() .
.
(文)(1)由an+bn=1(n∈N*)知bn=1-an,bn+1=1-an+1,
∴1-an+1=![]()
an-an+1=an·an+1,![]() =1,
=1,
∴数列![]() 是以
是以![]() =4为首项、以1为公差的等差数列.
=4为首项、以1为公差的等差数列.
∴![]() =4+n-1=n+3,∴an=
=4+n-1=n+3,∴an=![]() (n∈N*).
(n∈N*).
bn=1-an=1![]() (n∈N*).
(n∈N*).
(2)Sn=a1a2+a2a3+…+anan+1
=![]()
=![]() .
.
对任意n∈N*,不等式kSn>bn恒成立
∴![]() 即
即![]() 恒成立
恒成立
令f(n)=![]() ,
,
则f(1)=![]() ,f(2)=
,f(2)=![]() ,
,
又当n≥3时,n2>8,从而n2+3n>3n+8.
即![]() <1,∴f(n)<2.
<1,∴f(n)<2.
可见对任意n∈N*,f(n)的最大值为![]() ,故
,故![]() ,
,
∴k的最小值为16.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案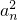 成等差数列.(1)求通项an;(2)设
成等差数列.(1)求通项an;(2)设 求f(n)的最大值.
求f(n)的最大值. 成等差数列.(1)求通项an;(2)设
成等差数列.(1)求通项an;(2)设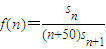 求f(n)的最大值.
求f(n)的最大值.