题目内容
运用对数的换底公式证明logamMn=
logaM（a＞0，且a≠1；M＞0，m≠0）．
| n | m |
分析：根据对数的换底公式进行证明即可．
解答：解：等式两边同时取以a为底数的对数得log?amMn=
=
=
log?aM．
| log?aMn |
| log?aam |
| nlog?aM |
| mlog?aa |
| n |
| m |
点评：本题主要考查对数的换底公式的应用，要求熟练掌握．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
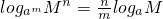（a＞0，且a≠1；M＞0，m≠0）．
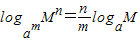（a＞0，且a≠1；M＞0，m≠0）．
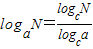（其中a＞0，a≠1，N＞0，c＞0，c≠1）．
．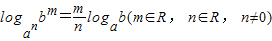