题目内容
已知函数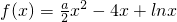 有两个极值点.
有两个极值点.
(I)求实数a的取值范围;
(II)若存在实数a,使函数f(x)在区间[b,b+2]上单调递增,求实数b的取值范围.
解:(Ⅰ)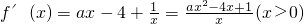 ,由题意:a≠0,又
,由题意:a≠0,又
①当a<0时,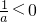 ,f'(x)=0两根异号,不合题意;
,f'(x)=0两根异号,不合题意;
②当a>0时, 可知△=16-4a>0,即0<a<4,
可知△=16-4a>0,即0<a<4,
此时由f′(x)=0得,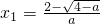 ,
,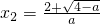 ,(4分)
,(4分)
由下表
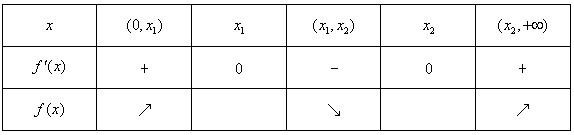
故当0<a<4时,函数f(x)的两个极值点.(6分)
(Ⅱ)结合(Ⅰ)可得“?a∈(0,4),使ax2-4x+1≥0对x∈[b,b+2]恒成立”,
即 a>-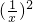 +
+ =-
=-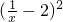 +4 恒成立,由[b,b+2]?(0,+∞)得b>0,
+4 恒成立,由[b,b+2]?(0,+∞)得b>0,
又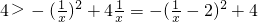 恒成立,
恒成立,
∴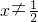 ,
,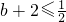 ,或
,或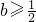 ,从而
,从而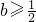 .(13分)
.(13分)
分析:(Ⅰ)先求出函数的导数,由题意知,导数等于0有两个正根,分a<0和a>0两种情况讨论.
(Ⅱ)由题意知,?a∈(0,4),使ax2-4x+1≥0对x∈[b,b+2]恒成立,即 a>-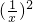 +
+ =-
=-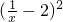 +4 恒成立,由
+4 恒成立,由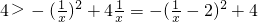 恒成立,故x≠
恒成立,故x≠ ,由b>0,根据
,由b>0,根据 不在区间[b,b+2]内,求出实数b的取值范围.
不在区间[b,b+2]内,求出实数b的取值范围.
点评:本题考查函数在某点存在极值的条件,利用导数判断函数的单调性的方法,以及函数的恒成立问题.
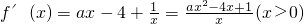 ,由题意:a≠0,又
,由题意:a≠0,又①当a<0时,
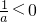 ,f'(x)=0两根异号,不合题意;
,f'(x)=0两根异号,不合题意;②当a>0时,
 可知△=16-4a>0,即0<a<4,
可知△=16-4a>0,即0<a<4,此时由f′(x)=0得,
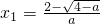 ,
,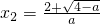 ,(4分)
,(4分)由下表
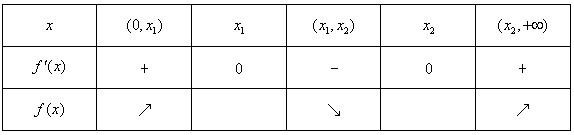
故当0<a<4时,函数f(x)的两个极值点.(6分)
(Ⅱ)结合(Ⅰ)可得“?a∈(0,4),使ax2-4x+1≥0对x∈[b,b+2]恒成立”,
即 a>-
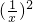 +
+ =-
=-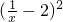 +4 恒成立,由[b,b+2]?(0,+∞)得b>0,
+4 恒成立,由[b,b+2]?(0,+∞)得b>0,又
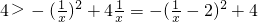 恒成立,
恒成立,∴
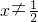 ,
,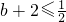 ,或
,或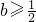 ,从而
,从而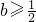 .(13分)
.(13分)分析:(Ⅰ)先求出函数的导数,由题意知,导数等于0有两个正根,分a<0和a>0两种情况讨论.
(Ⅱ)由题意知,?a∈(0,4),使ax2-4x+1≥0对x∈[b,b+2]恒成立,即 a>-
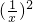 +
+ =-
=-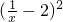 +4 恒成立,由
+4 恒成立,由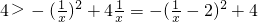 恒成立,故x≠
恒成立,故x≠ ,由b>0,根据
,由b>0,根据 不在区间[b,b+2]内,求出实数b的取值范围.
不在区间[b,b+2]内,求出实数b的取值范围.点评:本题考查函数在某点存在极值的条件,利用导数判断函数的单调性的方法,以及函数的恒成立问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目






 有两个极值点
有两个极值点 ,若
,若 ,则关于
,则关于 的方程
的方程 的不同实根个数为
的不同实根个数为 有两个极值点
有两个极值点 且
且 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 有两个极值点
有两个极值点 ,且直线
,且直线 与曲线
与曲线 相切于
相切于 点。
点。 和
和
 为整数时,求过
为整数时,求过