题目内容
(13分)已知数列![]() 满足:
满足:![]() 其中
其中![]() ,数列
,数列![]() 满足:
满足:![]()
(1)求![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在正数k,使得数列![]() 的每一项均为整数,如果不存在,说明理由,如果存在,求出所有的k.
的每一项均为整数,如果不存在,说明理由,如果存在,求出所有的k.
解析:(1)经过计算可知:![]()
![]() .
.
求得![]() .…………………………………………(4分)
.…………………………………………(4分)
(2)由条件可知:![]() .…………①
.…………①
类似地有:![]() .…………②
.…………②
①-②有:![]() .
.
即:![]() .
.
![]() 因此:
因此:![]()
![]()
即:![]() 故
故![]()
![]()
所以:![]() .…………………………………………(8分)
.…………………………………………(8分)
(3)假设存在正数![]() ,使得数列
,使得数列![]() 的每一项均为整数.
的每一项均为整数.
则由(2)可知: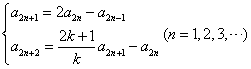 …………③
…………③
由![]() ,及
,及![]() 可知
可知![]() .
.
当![]() 时,
时,![]() 为整数,利用
为整数,利用![]() ,结合③式,反复递推,可知
,结合③式,反复递推,可知![]() ,
,![]() ,
,![]() ,
,![]() ,…均为整数.
,…均为整数.
当![]() 时,③变为
时,③变为 ………④
………④
我们用数学归纳法证明![]() 为偶数,
为偶数,![]() 为整数
为整数![]()
![]() 时,结论显然成立,假设
时,结论显然成立,假设![]() 时结论成立,这时
时结论成立,这时![]() 为偶数,
为偶数,![]() 为整数,故
为整数,故![]() 为偶数,
为偶数,![]() 为整数,所以
为整数,所以![]() 时,命题成立.
时,命题成立.
故数列![]() 是整数列.
是整数列.
综上所述,![]() 的取值集合是
的取值集合是![]() .………………………………………(13分)
.………………………………………(13分)

练习册系列答案
相关题目
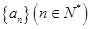 满足:
满足: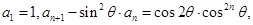 其中
其中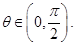
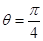 时,求
时,求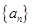 的通项公式;
的通项公式; 中,
中,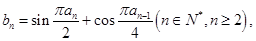 且
且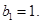 求证:对于
求证:对于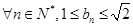 恒成立;
恒成立;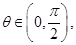 设
设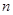 项和为
项和为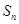 ,试比较
,试比较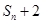 与
与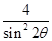 的大小.
的大小. 满足
满足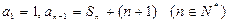 ,其中
,其中 为
为 项和,
项和,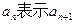 ;
;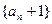 是等比数列;
是等比数列;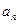 和
和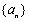 满足
满足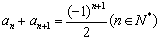 ,其中
,其中 ,试通过计算
,试通过计算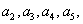 猜想
猜想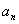 等于( )
等于( ) B.
B.
 D.
D.
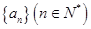 满足:
满足: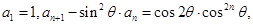 其中
其中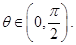
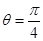 时,求
时,求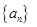 的通项公式;
的通项公式;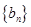 中,
中,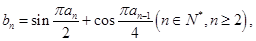 且
且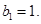 求证:对于
求证:对于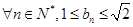 恒成立;
恒成立;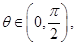 设
设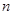 项和为
项和为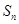 ,试比较
,试比较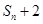 与
与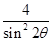 的大小.
的大小.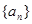 满足
满足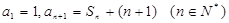 ,其中
,其中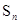 为
为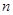 项和,
项和,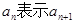 ;
;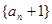 是等比数列;
是等比数列;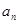 和
和