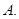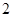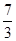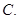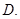题目内容
设等比数列![]() 的前
的前![]() 项和为
项和为![]() ,公比为
,公比为![]()
![]() 若
若![]() 成等差数列,求证:
成等差数列,求证:![]() 成等差数列;
成等差数列;
![]() 若
若![]() 为互不相等的正整数)成等差数列,试问数列
为互不相等的正整数)成等差数列,试问数列![]() 中是否存在不同的三项成等差数列?若存在,写出两组这三项,若不存在,请说明理由;
中是否存在不同的三项成等差数列?若存在,写出两组这三项,若不存在,请说明理由;
![]() 若
若![]() 为大于1的正整数,试问
为大于1的正整数,试问![]() 中是否存在一项
中是否存在一项![]() ,使得
,使得![]() 恰好可以表示为该数列中连续两项的和?请说明理由.
恰好可以表示为该数列中连续两项的和?请说明理由.
(本小题14分)
解:
(Ⅰ) 由![]() 成等差数列且
成等差数列且![]() 得:
得:
![]()
![]() ………………4分
………………4分
(Ⅱ) 由![]() 成等差数列且
成等差数列且![]() 得:
得:
![]()
![]()
可以写出多组:![]()
………………9分![]() 假设存在两项
假设存在两项![]() 使
使![]()
则有![]()
即![]() ………………11分
………………11分
当为奇数时,![]() 为奇数,
为奇数,![]() 为偶数,不成立;
为偶数,不成立;
当为偶数时,![]() 为偶数,
为偶数,![]() 为奇数,不成立.
为奇数,不成立.
![]() 中不存在项
中不存在项![]() ,使得
,使得![]() 恰好可以表示为该数列中连续两项的和. ………………14分
恰好可以表示为该数列中连续两项的和. ………………14分

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
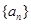 的前
的前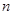 项和为
项和为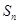 ,若
,若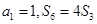 ,则
,则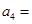 ______.
______.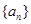 的前
的前 项和为
项和为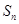 ,若
,若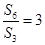 ,则
,则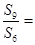 ( )
( )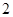 B.
B.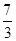 C.
C.
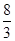 D.
D.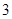
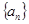 的前
的前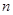 项和为
项和为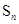 ,若
,若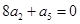 ,则下列式子中数值不能确定的是
,则下列式子中数值不能确定的是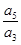 (B)
(B)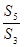 (C)
(C)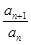 (D)
(D)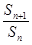
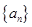 的前
的前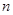 项和为
项和为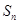 ,若
,若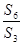 =3 ,则
=3 ,则 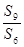 = ( )
= ( )