题目内容
已知 为锐角
为锐角 的三个内角,向量
的三个内角,向量 与
与 共线.
共线.
(1)求角 的大小;
的大小;
(2)求角 的取值范围
的取值范围
(3)求函数 的值域.
的值域.
 为锐角
为锐角 的三个内角,向量
的三个内角,向量 与
与 共线.
共线.(1)求角
 的大小;
的大小;(2)求角
 的取值范围
的取值范围(3)求函数
 的值域.
的值域.(1)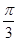 ;(2)
;(2)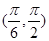 ;(3)(
;(3)(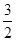 ,2]
,2]
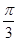 ;(2)
;(2)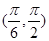 ;(3)(
;(3)(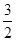 ,2]
,2]试题分析:(1)由向量平行的坐标形式及
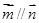 可列出关于角A的正弦的方程,求出
可列出关于角A的正弦的方程,求出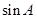 ,结合A为锐角,求出A角;(2)由(1)知A的值,从而求出B+C的值,将C用B表示出来,结合B、C都是锐角,列出关于B的不等式组,从而求出B的范围;(3)将函数式中C用B表示出来,化为B的函数,用降幂公式及辅助角公式化为一个角的三角函数,按照复合函数求值域的方法,结合(2)中B角的范围,求出内函数的值域,作为中间函数的定义域,利用三角函数图像求出中间函数的值域,作为外函数的定义域,再利用外函数的性质求出外函数的值域即为所求函数的值域.
,结合A为锐角,求出A角;(2)由(1)知A的值,从而求出B+C的值,将C用B表示出来,结合B、C都是锐角,列出关于B的不等式组,从而求出B的范围;(3)将函数式中C用B表示出来,化为B的函数,用降幂公式及辅助角公式化为一个角的三角函数,按照复合函数求值域的方法,结合(2)中B角的范围,求出内函数的值域,作为中间函数的定义域,利用三角函数图像求出中间函数的值域,作为外函数的定义域,再利用外函数的性质求出外函数的值域即为所求函数的值域.试题解析:(1)由题设知:
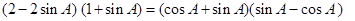
得
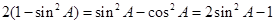 即
即 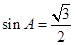
由△ABC是锐角三角形知:
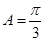 4分
4分(2)由(1)及题设知:
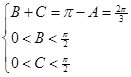 即
即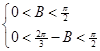 得
得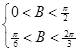
∴
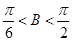 8分
8分(3)由(1)及题设知:
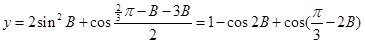
 , 10分
, 10分由(2)知:
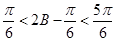
∴
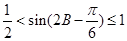 12分
12分∴
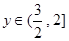
因此函数y=2sin2B+cos
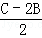 的值域为(
的值域为(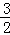 ,2] 14分
,2] 14分(其他写法参照给分)

练习册系列答案
相关题目
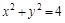 上一动点,
上一动点,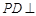 x轴于点D.记满足
x轴于点D.记满足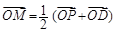 的动点M的轨迹为Γ.
的动点M的轨迹为Γ.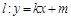 与轨迹Γ交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且
与轨迹Γ交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且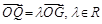 .
.
 的终边分别与单位圆交于A、B两点。
的终边分别与单位圆交于A、B两点。
 ,点B的横坐标为
,点B的横坐标为 ,求
,求 ;
; ,-2),
,-2), ,求
,求
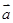 =(3,1),
=(3,1),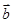 =(x,-3),且
=(x,-3),且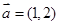 ,
, ,
,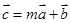 (
(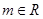 ),且
),且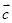 与
与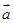 的夹角等于
的夹角等于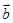 的夹角,则
的夹角,则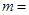 ( )
( )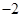
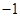
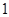
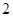
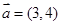 ,
,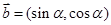 ,且
,且 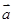 //
//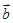 ,则
,则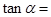 ( )
( )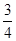
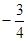
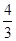
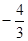
 则
则 的取值 ( )
的取值 ( )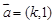 与
与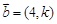 共线且方向相反,则
共线且方向相反,则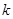 =( )
=( )

 互相垂直,则实数k的值是( )
互相垂直,则实数k的值是( )

