题目内容
已知 、
、 均为单位向量,(2
均为单位向量,(2 +
+ )•(
)•( -2
-2 )=-
)=- ,
, 与
与 的夹角为
的夹角为
- A.30°
- B.45°
- C.135°
- D.150°
D
分析:根据 、
、 均为单位向量,可得
均为单位向量,可得 =
= =1,将此代入(2
=1,将此代入(2 +
+ )•(
)•( -2
-2 )=-
)=- 并化简整理,得
并化简整理,得 =-
=- ,由此结合平面向量的夹角公式,即可算出
,由此结合平面向量的夹角公式,即可算出 与
与 的夹角的大小.
的夹角的大小.
解答:∵(2 +
+ )•(
)•( -2
-2 )=-
)=- ,
,
∴2 -3
-3 -2
-2 =-
=-
∵ 、
、 均为单位向量,可得
均为单位向量,可得 =
= =1
=1
∴2-3 -2=-
-2=- ,得
,得 =-
=-
设 与
与 的夹角为θ,则cosθ=
的夹角为θ,则cosθ= =-
=-
结合θ∈[0,π],可得θ=150°
故选:D
点评:本题给出单位向量 、
、 满足的数量积等式,求它们夹角的大小,着重考查了单位向量的概念、平面向量数量积的运算性质和向量的夹角公式等知识,属于基础题.
满足的数量积等式,求它们夹角的大小,着重考查了单位向量的概念、平面向量数量积的运算性质和向量的夹角公式等知识,属于基础题.
分析:根据
 、
、 均为单位向量,可得
均为单位向量,可得 =
= =1,将此代入(2
=1,将此代入(2 +
+ )•(
)•( -2
-2 )=-
)=- 并化简整理,得
并化简整理,得 =-
=- ,由此结合平面向量的夹角公式,即可算出
,由此结合平面向量的夹角公式,即可算出 与
与 的夹角的大小.
的夹角的大小.解答:∵(2
 +
+ )•(
)•( -2
-2 )=-
)=- ,
,∴2
 -3
-3 -2
-2 =-
=-
∵
 、
、 均为单位向量,可得
均为单位向量,可得 =
= =1
=1∴2-3
 -2=-
-2=- ,得
,得 =-
=-
设
 与
与 的夹角为θ,则cosθ=
的夹角为θ,则cosθ= =-
=-
结合θ∈[0,π],可得θ=150°
故选:D
点评:本题给出单位向量
 、
、 满足的数量积等式,求它们夹角的大小,着重考查了单位向量的概念、平面向量数量积的运算性质和向量的夹角公式等知识,属于基础题.
满足的数量积等式,求它们夹角的大小,着重考查了单位向量的概念、平面向量数量积的运算性质和向量的夹角公式等知识,属于基础题. 
练习册系列答案
相关题目



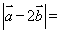












 与
与 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 等于( )
等于( ) B.
B. C.
C.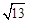 D.4
D.4 与
与 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,则|
,则| |=( )
|=( ) B.
B. C.
C.  D.
D.

 ,
,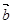 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为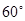 ,则
,则 _______.
_______.