题目内容
在平面斜坐标系 中
中 ,点
,点 的斜坐标定义为:“若
的斜坐标定义为:“若 (其中
(其中 分别为与斜坐标系的
分别为与斜坐标系的 轴,
轴, 轴同方向的单位向量),则点
轴同方向的单位向量),则点 的坐标为
的坐标为 ”.若
”.若 且动点
且动点 满足
满足 ,则点
,则点 在斜坐标系中的轨迹方程为( )
在斜坐标系中的轨迹方程为( )
A. | B. | C. | D. |
D.
解析试题分析:设M(x,y),∵F1(-1,0),F2(1,0),
∴由定义知|MF1|=|(x+1) +y
+y |,|MF2|=|(x-1)
|,|MF2|=|(x-1) +y
+y |,
|,
∵ ,∴(x+1)2+y2+2(x+1)×y×
,∴(x+1)2+y2+2(x+1)×y× =(x-1)2+y2+2(x-1)×y×
=(x-1)2+y2+2(x-1)×y×
整理得 x+y=0,故选D。
x+y=0,故选D。
考点:本题主要考查轨迹方程的求法,平面向量的数量积及模的计算。
点评:小综合题,本题以平面向量为载体,重点考查轨迹方程的求法。本题解法可谓之“直接法”,即从动点满足的几何条件出发,直接得到方程。

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
若两个非零向量 ,
,  满足|
满足| +
+ |=|
|=| -
- |=
|= |
| |,则向量
|,则向量 +
+ 与
与 -
- 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
已知O是锐角△ABC的外接圆圆心,∠A=60°, ,则m的值为( )
,则m的值为( )
A. | B. | C.1 | D. |
设向量 ,则
,则 的夹角等于( )
的夹角等于( )
A. | B. | C. | D. |
若平面向量a=(1,x)和b=(2x+3,-x)互相平行,其中x∈R,
则|a-b|=( )
A. | B.2或 | C.-2或0 | D.2或10 |
已知平面向量 ,
, ,则
,则
| A.-10 | B.10 | C.-20 | D.20 |
△ 外接圆的半径为
外接圆的半径为 ,圆心为
,圆心为 ,且
,且 ,
,  ,则
,则 等于
等于
A. | B. | C. | D.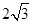 |
已知两个非零向量 与
与 ,定义
,定义 ,其中
,其中 为
为 与
与 的夹角.若
的夹角.若 ,
,  ,则
,则 的值为
的值为
A. | B. | C. | D. |
 ,
, ,且
,且 ,
, ,则向量
,则向量 =_________.
=_________.