题目内容
已知数列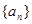 满足
满足 ,又
,又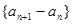 成等差数列
成等差数列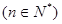 则
则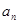 等于 .
等于 .
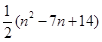 .
.
解析试题分析: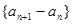 成等差数列,一般我们称数列
成等差数列,一般我们称数列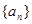 为一阶等差数列,求它的通项公式的方法是的累加法,
为一阶等差数列,求它的通项公式的方法是的累加法,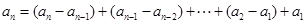 ,由已知
,由已知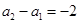 ,
,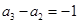 ,又
,又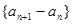 成等差数列,∴
成等差数列,∴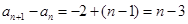 .从而
.从而 =
=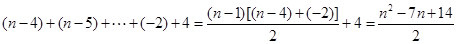 .
.
考点:数列的求和.

练习册系列答案
相关题目
数列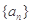 的前n项和
的前n项和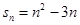 ,则通项公式
,则通项公式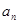 为( )
为( )
A.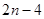 | B.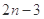 | C.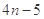 | D.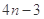 |
题目内容
已知数列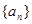 满足
满足 ,又
,又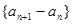 成等差数列
成等差数列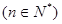 则
则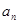 等于 .
等于 .
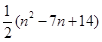 .
.
解析试题分析: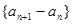 成等差数列,一般我们称数列
成等差数列,一般我们称数列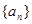 为一阶等差数列,求它的通项公式的方法是的累加法,
为一阶等差数列,求它的通项公式的方法是的累加法,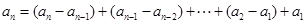 ,由已知
,由已知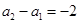 ,
,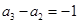 ,又
,又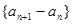 成等差数列,∴
成等差数列,∴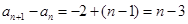 .从而
.从而 =
=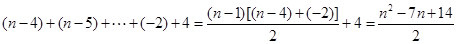 .
.
考点:数列的求和.

数列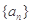 的前n项和
的前n项和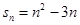 ,则通项公式
,则通项公式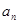 为( )
为( )
A.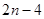 | B.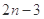 | C.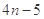 | D.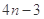 |