题目内容
设M是椭圆C: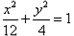 上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程。 上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程。 |
解:设点的坐标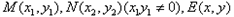 , ,则  , ,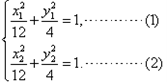 , ,由(1)-(2)可得 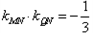 , ,又MN⊥MQ, 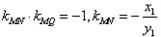 , ,所以 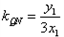 ,直线QN的方程为 ,直线QN的方程为 , ,又直线PT的方程为 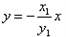 , ,从而得 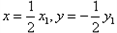 , ,所以 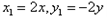 , ,代入(1)可得 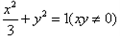 ,此即为所求的轨迹方程。 ,此即为所求的轨迹方程。 |

练习册系列答案
相关题目
题目内容
设M是椭圆C: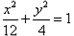 上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程。 上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程。 |
解:设点的坐标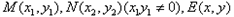 , ,则  , ,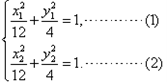 , ,由(1)-(2)可得 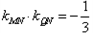 , ,又MN⊥MQ, 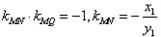 , ,所以 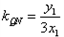 ,直线QN的方程为 ,直线QN的方程为 , ,又直线PT的方程为 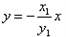 , ,从而得 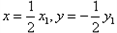 , ,所以 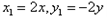 , ,代入(1)可得 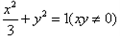 ,此即为所求的轨迹方程。 ,此即为所求的轨迹方程。 |
