题目内容
自平面α外一点P,向平面α引垂线PO及两条斜线段PA、PB,它们在平面α内的射影长分别为2cm和12cm,且两条斜线与平面α所成的角相差45°,则垂线段PO长为( )
分析:由题意,设∠PBO=α,则∠PAO=45°+α,从而PO=2tan(α+45°)=12tanα,故可求tanα,进而可求PO的长;
解答:解:由题意,设∠PBO=α,则∠PAO=45°+α
∴PO=2tan(α+45°)=12tanα,
∴tanα=
或 tanα=
∴P0=6或4
故选C.
∴PO=2tan(α+45°)=12tanα,
∴tanα=
| 1 |
| 2 |
| 1 |
| 3 |
∴P0=6或4
故选C.
点评:本题以线面角为载体,考查线面角,考查射影,考查和角的正切公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
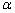 外一点P,向平面
外一点P,向平面