题目内容
若
，而a，b，c各不相等，求x+y+z的值．
【答案】分析：本题根据
，设出
=t，从而将x，y，z用a，b，c，t来表示即可
解答：解：设
=t，
则有x=（a-b）t，y=（b-c）tz=（c-a）t
由此可得：x+y+z=（a-b）t+（b-c）t+（c-a）t=0．
点评：本题考查了换元的解题思想方法，属于基础题．
，设出=t，从而将x，y，z用a，b，c，t来表示即可解答：解：设
=t，则有x=（a-b）t，y=（b-c）tz=（c-a）t
由此可得：x+y+z=（a-b）t+（b-c）t+（c-a）t=0．
点评：本题考查了换元的解题思想方法，属于基础题．
练习册系列答案
相关题目
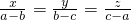，而a，b，c各不相等，求x+y+z的值．