题目内容
曲线C是平面内与两个定点F1(-1,0)和F2(1,0)的距离的积等于常数a2(a>1)的点的轨迹.给出下列三个结论:①曲线C过坐标原点;
②曲线C关于坐标原点对称;
③若点P在曲线C上,则△F1PF2的面积不大于
 a2.
a2.其中,所有正确结论的序号是 .
【答案】分析:由题意曲线C是平面内与两个定点F1(-1,0)和F2(1,0)的距离的积等于常数a2(a>1),利用直接法,设动点坐标为(x,y),及可得到动点的轨迹方程,然后由方程特点即可加以判断.
解答:解:对于①,由题意设动点坐标为(x,y),则利用题意及两点间的距离公式的得: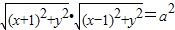 ?[(x+1)2+y2]•[(x-1)2+y2]=a4(1)将原点代入验证,此方程不过原点,所以①错;
?[(x+1)2+y2]•[(x-1)2+y2]=a4(1)将原点代入验证,此方程不过原点,所以①错;
对于②,把方程中的x被-x代换,y被-y 代换,方程不变,故此曲线关于原点对称.②正确;
对于③,由题意知点P在曲线C上,则△F1PF2的面积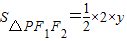 ,
,
由(1)式平方化简的:y4+[(x+1)2+(x-1)2]y2+(x2-1)2-a4=0⇒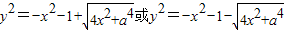 (舍)
(舍)
把三角形的面积式子平方得: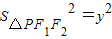 对于
对于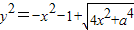 (2)
(2)
令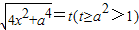 ⇒
⇒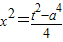
代入(2)得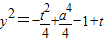 =
=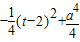 ≤
≤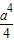 ,
,
故可知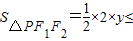
 a2 所以③正确.
a2 所以③正确.
故答案为:②③
点评:此题重点考查了利用直接法求出动点的轨迹方程,并化简,利用方程判断曲线的对称性及利用解析式选择换元法求出值域.
解答:解:对于①,由题意设动点坐标为(x,y),则利用题意及两点间的距离公式的得:
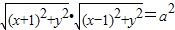 ?[(x+1)2+y2]•[(x-1)2+y2]=a4(1)将原点代入验证,此方程不过原点,所以①错;
?[(x+1)2+y2]•[(x-1)2+y2]=a4(1)将原点代入验证,此方程不过原点,所以①错;对于②,把方程中的x被-x代换,y被-y 代换,方程不变,故此曲线关于原点对称.②正确;
对于③,由题意知点P在曲线C上,则△F1PF2的面积
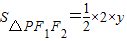 ,
,由(1)式平方化简的:y4+[(x+1)2+(x-1)2]y2+(x2-1)2-a4=0⇒
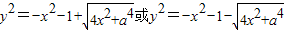 (舍)
(舍) 把三角形的面积式子平方得:
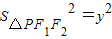 对于
对于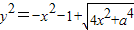 (2)
(2)令
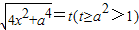 ⇒
⇒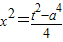
代入(2)得
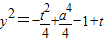 =
=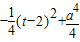 ≤
≤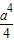 ,
,故可知
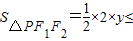
 a2 所以③正确.
a2 所以③正确.故答案为:②③
点评:此题重点考查了利用直接法求出动点的轨迹方程,并化简,利用方程判断曲线的对称性及利用解析式选择换元法求出值域.

练习册系列答案
相关题目
 a2.
a2.