题目内容
已知动点P到点F(2,0)的距离与它到直线x=1的距离之比为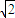 .
.(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设点P的轨迹为曲线C,过点F作互相垂直的两条直线l1、l2,l1交曲线C于A、B两点,l2交曲线C于M、N两点.求证:
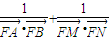 为定值.
为定值.
【答案】分析:(1)设出动点P的坐标,直接利用条件写方程,化简.
(2)当当直线l1,l2之一与x轴垂直时,易求此定值,当直线l1,l2都不与x轴垂直时,设出直线l1的方程,得到l2的方程,将l1的方程于双曲线的方程联立,利用根与系数的关系计算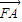 与
与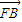 ,进而计算
,进而计算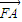 •
•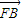 的值,同理计算
的值,同理计算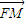 •
•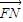 的值,即得结果.
的值,即得结果.
解答: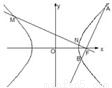 解:(Ⅰ)设P(x,y),由题意得:
解:(Ⅰ)设P(x,y),由题意得: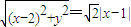 .
.
所以点P的轨迹方程为x2-y2=2.(4分)
(Ⅱ)当直线l1,l2之一与x轴垂直,不妨设l1与x轴垂直,此时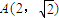 ,
,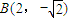 ,
,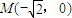 ,
,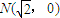 ,
,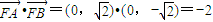 ,
,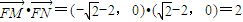 ,
,
所以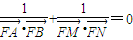 .(6分)
.(6分)
当直线l1,l2都不与x轴垂直时,
由题意设直线l1为y=k(x-2)k≠0,
则l2的方程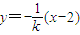 ,
,
由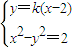 得(1-k2)x2+4k2x-4k2-2=0.(7分)
得(1-k2)x2+4k2x-4k2-2=0.(7分)
因为l1交双曲线C于A、B两点,
所以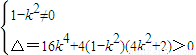 解得k≠±1.(8分)
解得k≠±1.(8分)
设A(x1,y1),B(x2,y2),
则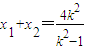 ,
,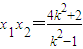 ,y1=k(x1-2),y2=k(x2-2),
,y1=k(x1-2),y2=k(x2-2),
因为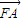 =(x1-2,y1),
=(x1-2,y1),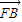 =(x2-2,y2),
=(x2-2,y2),
所以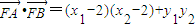 =(1+k2)[x1x2-2(x1+x2)+4]=
=(1+k2)[x1x2-2(x1+x2)+4]=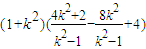 =
=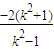 (11分)
(11分)
同理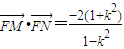 ,(12分)
,(12分)
所以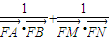 =
=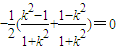 ,
,
即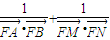 为定值0.(14分)
为定值0.(14分)
点评:本题考查轨迹方程的求法、直线与圆锥曲线的综合应用.
(2)当当直线l1,l2之一与x轴垂直时,易求此定值,当直线l1,l2都不与x轴垂直时,设出直线l1的方程,得到l2的方程,将l1的方程于双曲线的方程联立,利用根与系数的关系计算
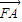 与
与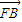 ,进而计算
,进而计算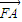 •
•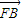 的值,同理计算
的值,同理计算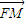 •
•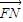 的值,即得结果.
的值,即得结果.解答:
 解:(Ⅰ)设P(x,y),由题意得:
解:(Ⅰ)设P(x,y),由题意得: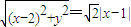 .
.所以点P的轨迹方程为x2-y2=2.(4分)
(Ⅱ)当直线l1,l2之一与x轴垂直,不妨设l1与x轴垂直,此时
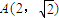 ,
,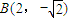 ,
,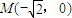 ,
,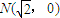 ,
,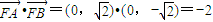 ,
,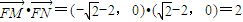 ,
,所以
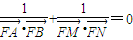 .(6分)
.(6分)当直线l1,l2都不与x轴垂直时,
由题意设直线l1为y=k(x-2)k≠0,
则l2的方程
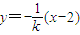 ,
,由
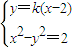 得(1-k2)x2+4k2x-4k2-2=0.(7分)
得(1-k2)x2+4k2x-4k2-2=0.(7分)因为l1交双曲线C于A、B两点,
所以
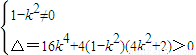 解得k≠±1.(8分)
解得k≠±1.(8分)设A(x1,y1),B(x2,y2),
则
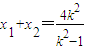 ,
,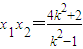 ,y1=k(x1-2),y2=k(x2-2),
,y1=k(x1-2),y2=k(x2-2),因为
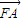 =(x1-2,y1),
=(x1-2,y1),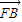 =(x2-2,y2),
=(x2-2,y2),所以
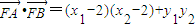 =(1+k2)[x1x2-2(x1+x2)+4]=
=(1+k2)[x1x2-2(x1+x2)+4]=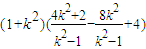 =
=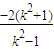 (11分)
(11分)同理
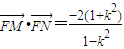 ,(12分)
,(12分)所以
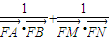 =
=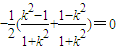 ,
,即
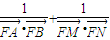 为定值0.(14分)
为定值0.(14分)点评:本题考查轨迹方程的求法、直线与圆锥曲线的综合应用.

练习册系列答案
相关题目
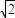 .
.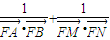 为定值.
为定值.