题目内容
设椭圆方程为 ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足 ,点N的坐标为
,点N的坐标为 ,当l绕点M旋转时,求:
,当l绕点M旋转时,求:(1)动点P的轨迹方程;
(2)
 的最小值与最大值.
的最小值与最大值.
【答案】分析:(1)设出直线l的方程,A,B的坐标,联立直线与椭圆的方程,利用韦达定理表示出x1+x2,利用直线方程表示出y1+y2,然后利用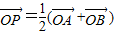 求得
求得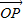 的坐标,设出P的坐标,然后联立方程消去参数k求得x和y的关系式,P点轨迹可得.
的坐标,设出P的坐标,然后联立方程消去参数k求得x和y的关系式,P点轨迹可得.
(2)根据点P的轨迹方程求得x的范围,利用两点间的距离公式求得|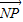 |,利用二次函数的性质和x的范围求得其最大和最小值.
|,利用二次函数的性质和x的范围求得其最大和最小值.
解答:解:(1)直线l过点M(0,1)设其斜率为k,则l的方程为y=kx+1.
记A(x1,y1)、B(x2,y2),由题设可得点A、B的坐标是方程组
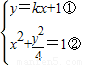 的解.
的解.
将①代入②并化简得,(4+k2)x2+2kx-3=0,所以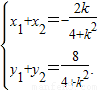 ,
,
于是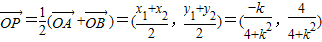 .
.
设点P的坐标为(x,y),则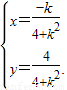 消去参数k得4x2+y2-y=0③
消去参数k得4x2+y2-y=0③
当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,所以点P的轨迹方
程为4x2+y2-y=0.
(2)解:由点P的轨迹方程知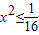 ,即
,即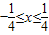 .所以
.所以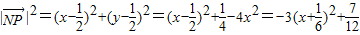
故当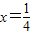 ,
,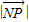 取得最小值,最小值为
取得最小值,最小值为 ;当
;当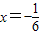 时,
时,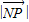 取得最大值,
取得最大值,
最大值为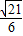 .
.
点评:本小题主要考查平面向量的概念、直线方程的求法、椭圆的方程和性质等基础知识,以及轨迹的求法与应用、曲线与方程的关系等解析几何的基本思想和综合解题能力.
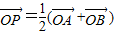 求得
求得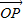 的坐标,设出P的坐标,然后联立方程消去参数k求得x和y的关系式,P点轨迹可得.
的坐标,设出P的坐标,然后联立方程消去参数k求得x和y的关系式,P点轨迹可得.(2)根据点P的轨迹方程求得x的范围,利用两点间的距离公式求得|
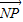 |,利用二次函数的性质和x的范围求得其最大和最小值.
|,利用二次函数的性质和x的范围求得其最大和最小值.解答:解:(1)直线l过点M(0,1)设其斜率为k,则l的方程为y=kx+1.
记A(x1,y1)、B(x2,y2),由题设可得点A、B的坐标是方程组
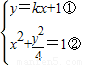 的解.
的解.将①代入②并化简得,(4+k2)x2+2kx-3=0,所以
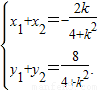 ,
,于是
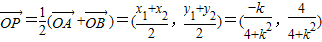 .
.设点P的坐标为(x,y),则
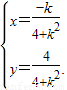 消去参数k得4x2+y2-y=0③
消去参数k得4x2+y2-y=0③当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,所以点P的轨迹方
程为4x2+y2-y=0.
(2)解:由点P的轨迹方程知
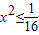 ,即
,即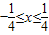 .所以
.所以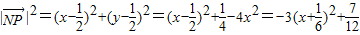
故当
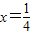 ,
,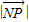 取得最小值,最小值为
取得最小值,最小值为 ;当
;当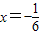 时,
时,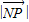 取得最大值,
取得最大值,最大值为
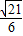 .
.点评:本小题主要考查平面向量的概念、直线方程的求法、椭圆的方程和性质等基础知识,以及轨迹的求法与应用、曲线与方程的关系等解析几何的基本思想和综合解题能力.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足 ,点N的坐标为
,点N的坐标为 ,当l绕点M旋转时,求:
,当l绕点M旋转时,求: 的最小值与最大值.
的最小值与最大值. ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足 ,点N的坐标为
,点N的坐标为 ,当l绕点M旋转时,求:
,当l绕点M旋转时,求: 的最小值与最大值.
的最小值与最大值. ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足 ,点N的坐标为
,点N的坐标为 ,当l绕点M旋转时,求:
,当l绕点M旋转时,求: 的最小值与最大值.
的最小值与最大值. ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足 ,点N的坐标为
,点N的坐标为 ,当l绕点M旋转时,求:
,当l绕点M旋转时,求: 的最小值与最大值.
的最小值与最大值.