题目内容
设椭圆E: 的离心率为e=
的离心率为e= ,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为
,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为 .
.
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ?若存在,求出该圆的方程;若不存在说明理由.
?若存在,求出该圆的方程;若不存在说明理由.
解:(I)依题意知,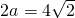 ,∴
,∴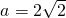 .----------(1分)
.----------(1分)
∵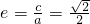 ,∴
,∴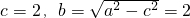 .---------------(3分)
.---------------(3分)
∴所求椭圆E的方程为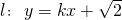 .----------(4分)
.----------(4分)
(II)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ,
,
设该圆的切线方程为y=kx+m----------(5分)
代入椭圆方程,消去y可得:(1+2k2)x2+4kmx+2m2-8=0,----------------(6分)
则△=8(8k2-m2+4)>0,即8k2-m2+4>0,x1+x2=-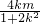 ,x1x2=
,x1x2=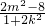 ,-------------------(7分)
,-------------------(7分)
∴y1y2=(kx1+m)(kx2+m)=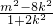
要使 ,需使x1x2+y1y2=0,即
,需使x1x2+y1y2=0,即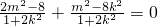 ,-------------------(9分)
,-------------------(9分)
所以3m2-8k2-8=0,所以 -------------------(10分)
-------------------(10分)
又8k2-m2+4>0,所以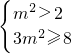 ,∴
,∴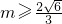 或
或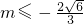 ,
,
因为直线y=kx+m为圆心在原点的圆的一条切线,所以圆的半径为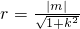 ,
,
即: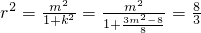 ,∴r=
,∴r= ,∴所求的圆的方程为:
,∴所求的圆的方程为: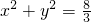 ,-------------(12分)
,-------------(12分)
而当切线的斜率不存在时切线为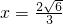 与椭圆
与椭圆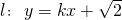 的两个交点为(
的两个交点为( ,
,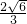 )或
)或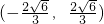 满足
满足 .-----------------(13分)
.-----------------(13分)
综上所述,存在圆心在原点的圆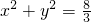 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 .----------------(14分)
.----------------(14分)
分析:(I)根据离心率为e= ,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为
,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为 ,求出几何量,从而可求椭圆E的方程;
,求出几何量,从而可求椭圆E的方程;
(II)先假设存在,设该圆的切线方程代入椭圆方程,利用韦达定理及 ,可确定m的范围及所求的圆的方程,验证当切线的斜率不存在时,结论也成立.
,可确定m的范围及所求的圆的方程,验证当切线的斜率不存在时,结论也成立.
点评:本题考查椭圆的标准方程,考查 直线与椭圆的位置关系,考查向量知识的运用,考查韦达定理,考查学生的计算能力,属于中档题.
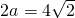 ,∴
,∴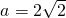 .----------(1分)
.----------(1分)∵
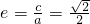 ,∴
,∴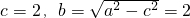 .---------------(3分)
.---------------(3分)∴所求椭圆E的方程为
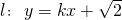 .----------(4分)
.----------(4分)(II)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
 ,
,设该圆的切线方程为y=kx+m----------(5分)
代入椭圆方程,消去y可得:(1+2k2)x2+4kmx+2m2-8=0,----------------(6分)
则△=8(8k2-m2+4)>0,即8k2-m2+4>0,x1+x2=-
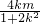 ,x1x2=
,x1x2=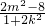 ,-------------------(7分)
,-------------------(7分)∴y1y2=(kx1+m)(kx2+m)=
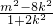
要使
 ,需使x1x2+y1y2=0,即
,需使x1x2+y1y2=0,即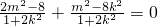 ,-------------------(9分)
,-------------------(9分)所以3m2-8k2-8=0,所以
 -------------------(10分)
-------------------(10分)又8k2-m2+4>0,所以
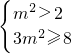 ,∴
,∴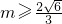 或
或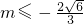 ,
,因为直线y=kx+m为圆心在原点的圆的一条切线,所以圆的半径为
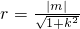 ,
,即:
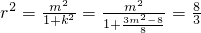 ,∴r=
,∴r= ,∴所求的圆的方程为:
,∴所求的圆的方程为: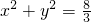 ,-------------(12分)
,-------------(12分)而当切线的斜率不存在时切线为
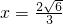 与椭圆
与椭圆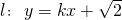 的两个交点为(
的两个交点为( ,
,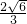 )或
)或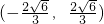 满足
满足 .-----------------(13分)
.-----------------(13分)综上所述,存在圆心在原点的圆
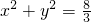 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 .----------------(14分)
.----------------(14分)分析:(I)根据离心率为e=
 ,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为
,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为 ,求出几何量,从而可求椭圆E的方程;
,求出几何量,从而可求椭圆E的方程;(II)先假设存在,设该圆的切线方程代入椭圆方程,利用韦达定理及
 ,可确定m的范围及所求的圆的方程,验证当切线的斜率不存在时,结论也成立.
,可确定m的范围及所求的圆的方程,验证当切线的斜率不存在时,结论也成立.点评:本题考查椭圆的标准方程,考查 直线与椭圆的位置关系,考查向量知识的运用,考查韦达定理,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,右焦点到右准线的距离为3.
,右焦点到右准线的距离为3. ,0)作倾角为锐角的直线l交椭圆于A,B两点,若
,0)作倾角为锐角的直线l交椭圆于A,B两点,若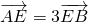 ,求l的方程.
,求l的方程. 的离心率为
的离心率为 ,左焦点为F,过原点的直线l交椭圆于M,N两点,△FMN面积的最大值为1.
,左焦点为F,过原点的直线l交椭圆于M,N两点,△FMN面积的最大值为1. .
.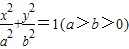 的离心率为e=
的离心率为e=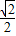 ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4. ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围. 的离心率为e=
的离心率为e= ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4. ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围.