题目内容
对于集合 (
( ),定义集合
),定义集合
 ,记集合
,记集合 中的元素个数为
中的元素个数为 .
.
(1)若集合 ,则
,则 ;
;
(2)若 是公差大于零的等差数列, 则
是公差大于零的等差数列, 则 (用含
(用含 的代数式表示).
的代数式表示).
(1)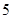 ;(2)
;(2)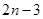
解析试题分析:因为对于集合
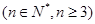 ,定义集合
,定义集合
 ,记集合
,记集合 中的元素个数为
中的元素个数为 ,即集合
,即集合 中的元素是集合
中的元素是集合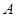 中任意两个元素的和的集合,所以(1)当
中任意两个元素的和的集合,所以(1)当 时,
时,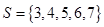 ,
,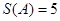 ;(2)由题意,集合
;(2)由题意,集合 中最小项为
中最小项为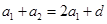 ,最大项为
,最大项为 ,对任意的
,对任意的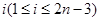 ,如果
,如果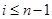 ,则可取
,则可取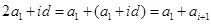
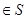 ,若
,若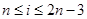 ,可取
,可取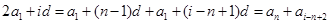 ,显然由于
,显然由于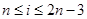 ,有
,有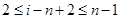 ,即
,即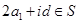 ,所以
,所以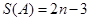 .
.
考点:1.集合的含义.2.等差数列的通项公式.

练习册系列答案
相关题目
若集合 ,则
,则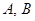 之间的关系是( )
之间的关系是( )
A. | B. | C. | D.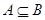 |
已知集合 ,
, ,那么
,那么 ( )
( )
A. | B. | C. | D. |
 ,则
,则 .
. ,
,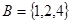 则集合
则集合 _______.
_______.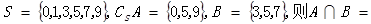 .
. ,
, ,
, ,则
,则 的值等于 .
的值等于 .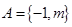 ,
, ,若
,若 ,则实数
,则实数 的取值范围是 .
的取值范围是 . ,k∈N},B={x|0≤x≤6,x∈Q},则A∩B=________.
,k∈N},B={x|0≤x≤6,x∈Q},则A∩B=________.