题目内容
(本题满分12分)
如图,在四棱锥 中,
中, 底面
底面 ,
, ,
, ,
, 是
是 的中点.
的中点.
(Ⅰ)证明 ;
;
(Ⅱ)证明 平面
平面 ;
;
(Ⅰ)由线面垂直得线线垂直:因 底面
底面 ,所以
,所以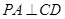 .
. ,
,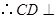 平面
平面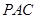 .
.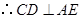 .(Ⅱ)由线线垂直得线面垂直:易得
.(Ⅱ)由线线垂直得线面垂直:易得 .
. 是
是 的中点,
的中点,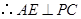 .由(Ⅰ)知,
.由(Ⅰ)知,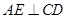 ,所以
,所以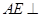 平面
平面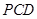 .
. 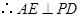 .
.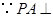 底面
底面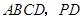 在底面
在底面 内的射影是
内的射影是 ,
,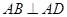 ,
,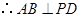 .得
.得 平面
平面 .
.
解析试题分析:(Ⅰ)证明:在四棱锥 中,因
中,因 底面
底面 ,
,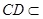 平面
平面 ,故
,故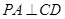 .
.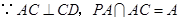 ,
,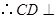 平面
平面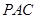 .
.
而 平面
平面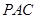 ,
,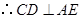 .
.
(Ⅱ)证明:由 ,
,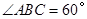 ,可得
,可得 .
. 是
是 的中点,
的中点,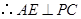 .
.
由(Ⅰ)知,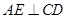 ,且
,且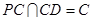 ,所以
,所以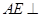 平面
平面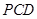 .
.
而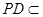 平面
平面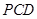 ,
,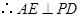 .
.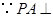 底面
底面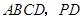 在底面
在底面 内的射影是
内的射影是 ,
,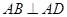 ,
,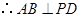 .
.
又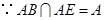 ,综上得
,综上得 平面
平面 .
.
考点:本题考查了空间中的线面关系
点评:对于立体几何问题的证明问题,要求我们熟练应用课本上的定理、性质、结论等,考查了学生的空间想象能力

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目


 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
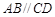 ,
,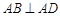 ,且
,且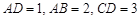 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且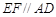 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为 .
.
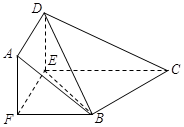
 平面BDE;
平面BDE; 的所有棱长都为2,
的所有棱长都为2, 为
为 中点,
中点, 平面
平面

 平面
平面 ;
; 的余弦值;
的余弦值; 到平面
到平面 ,
, ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使 且
且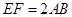 ,得一简单组合体
,得一简单组合体 如图2示,已知
如图2示,已知 分别为
分别为 的中点.
的中点.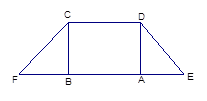

 平面
平面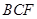 ;
;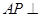
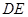 ;
;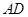 多长时,平面
多长时,平面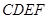 与平面
与平面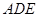 所成的锐二面角为
所成的锐二面角为 ?
? 中,
中, ,
, ,
,
 面
面
 的余弦值.
的余弦值. 中,E是BC的中点,F是
中,E是BC的中点,F是 的中点
的中点

 的平面角的余弦值.
的平面角的余弦值. 的侧面
的侧面 是菱形,
是菱形,


 平面
平面 ;
; 是
是 上的点,且
上的点,且 平面
平面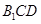 ,求
,求 的值.
的值.