题目内容
一个边长为12cm的正方形铁片，铁片的四角截去四个边长都为x的小正方形，然后做成一个无盖方盒，要使方盒的容积最大，x的值应为________．
2cm
分析：先表示出方盒的容积，再用基本不等式求最值．
解答：由题意，方盒的高xcm，长、宽都是（12-2x）cm
∴V=（12-2x）2×x=4（6-x）2×x
∵2x+（6-x）+（6-x）≥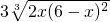
∴（6-x）2×x≤32（当且仅当6-x=2x，即x=2时取等号）
∴x=2cm时，方盒的容积最大
故答案为：2cm
点评：本题考查函数模型的构建，考查基本不等式的运用，属于中档题．
分析：先表示出方盒的容积，再用基本不等式求最值．
解答：由题意，方盒的高xcm，长、宽都是（12-2x）cm
∴V=（12-2x）2×x=4（6-x）2×x
∵2x+（6-x）+（6-x）≥
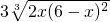
∴（6-x）2×x≤32（当且仅当6-x=2x，即x=2时取等号）
∴x=2cm时，方盒的容积最大
故答案为：2cm
点评：本题考查函数模型的构建，考查基本不等式的运用，属于中档题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
．