题目内容
已知函数 是定义在R上的奇函数,若对于任意给
是定义在R上的奇函数,若对于任意给
定的不等实数 、
、 ,不等式
,不等式
恒成立,则不等式 的解集为( ※ )
的解集为( ※ )
 是定义在R上的奇函数,若对于任意给
是定义在R上的奇函数,若对于任意给定的不等实数
 、
、 ,不等式
,不等式
恒成立,则不等式
 的解集为( ※ )
的解集为( ※ )A. | B. | C. | D. |
B
分析:先利用不等式(x1-x2)[f(x1)-f(x2)]<0恒成立得到函数f(x)是定义在R上的减函数;再利用函数f(x+1)是定义在R上的奇函数得到函数f(x)过(1,0)点,二者相结合即可求出不等式f(1-x)<0的解集.
解:由不等式(x1-x2)[f(x1)-f(x2)]<0恒成立得,函数f(x)是定义在R上的减函数①.
又因为函数f(x+1)是定义在R上的奇函数,所以有函数f(x+1)过点(0,0);
故函数f(x)过点(1,0)②.
①②相结合得:x>1时,f(x)<0.
故不等式f(1-x)<0转化为1-x>1?x<0.
故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,设函数
,设函数 满足:对于任意大于
满足:对于任意大于 的正整数
的正整数 ,
,
 ,则其中一个函数
,则其中一个函数 在
在 处的函数值为 ;
处的函数值为 ; ,且当
,且当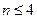 时,
时,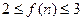 ,则不同的函数
,则不同的函数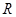 上的偶函数
上的偶函数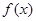 ,对于任意的
,对于任意的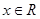 都满足:
都满足: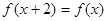 ,当
,当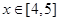 时
时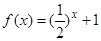 ,则( )
,则( )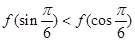
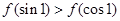
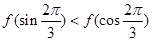
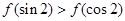
 的一个正数零点附近的函数值用二分法计算,其参
的一个正数零点附近的函数值用二分法计算,其参
 的一个近似根(精确到0.1)为
的一个近似根(精确到0.1)为  的图像大致是( )
的图像大致是( )
 -k(x-3)+4=0有两个不同的解时,实数k的取值范围是( )
-k(x-3)+4=0有两个不同的解时,实数k的取值范围是( )
 ,+∞)
,+∞) )
)
 为区间
为区间 上的连续函数,且恒有
上的连续函数,且恒有 ,可以用随机模拟
,可以用随机模拟 ,先产生两组(每组
,先产生两组(每组 个)区间
个)区间 和
和 ,由此得到
,由此得到 。再数出其中满足
。再数出其中满足 的点数
的点数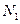 ,那么由随机模拟方法计算积分
,那么由随机模拟方法计算积分 有零点,则实数
有零点,则实数 的取值范围是
的取值范围是  若有
若有 则
则 的取值范围为( )
的取值范围为( )