题目内容
已知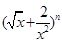 的展开式中,第
的展开式中,第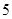 项的系数与第
项的系数与第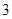 项的系数之比是10:1,求展开式中,
项的系数之比是10:1,求展开式中,
(1)含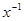 的项;
的项;
(2)系数最大的项.
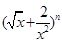 的展开式中,第
的展开式中,第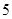 项的系数与第
项的系数与第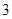 项的系数之比是10:1,求展开式中,
项的系数之比是10:1,求展开式中,(1)含
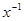 的项;
的项;(2)系数最大的项.
(1)T3=112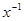 ;(2)
;(2)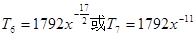 .
.
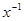 ;(2)
;(2)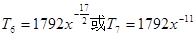 .
.本题先通过二项式展开式系数公式列出关于n的方程,求出n,然后再利用展开式通项求出含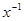 的项;然后再利用系数最大的思想列出关于项数的不等式求解即可
的项;然后再利用系数最大的思想列出关于项数的不等式求解即可
解: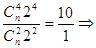 n=8或-3(舍去) (3分)
n=8或-3(舍去) (3分)
由通项公式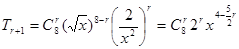 ,(6分)
,(6分)
(1)当r=2时,取到含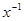 的项,即T3=112
的项,即T3=112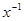 (8分)
(8分)
(2)由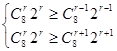 ,得
,得 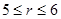 , 所以
, 所以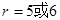 , (12分)
, (12分)
即系数最大的项为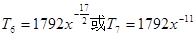 (14分)
(14分)
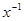 的项;然后再利用系数最大的思想列出关于项数的不等式求解即可
的项;然后再利用系数最大的思想列出关于项数的不等式求解即可解:
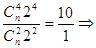 n=8或-3(舍去) (3分)
n=8或-3(舍去) (3分)由通项公式
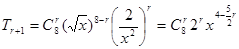 ,(6分)
,(6分)(1)当r=2时,取到含
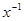 的项,即T3=112
的项,即T3=112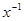 (8分)
(8分)(2)由
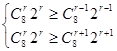 ,得
,得 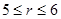 , 所以
, 所以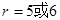 , (12分)
, (12分)即系数最大的项为
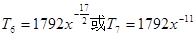 (14分)
(14分)
练习册系列答案
相关题目
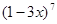 的展开式中系数和为m,二项式系数和为n,则
的展开式中系数和为m,二项式系数和为n,则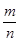 的值为( )
的值为( )


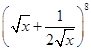 的展开式中常数项为
的展开式中常数项为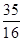


 ,且
,且 .
. 的值;
的值;  的值.
的值. 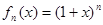 ,
,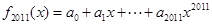 ,求
,求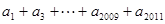 的值;
的值;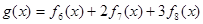 ,求
,求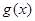 中含
中含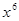 项的系数
项的系数 展开式中常数项为
展开式中常数项为 , 则此展开式中各项系数的和等于 .
, 则此展开式中各项系数的和等于 .
 的展开式中
的展开式中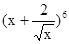 的展开式中常数项是( )
的展开式中常数项是( ) ;
; ;
; 的展开式中
的展开式中  的系数为A,则A= .
的系数为A,则A= .