题目内容
已知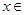
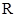 ,用符号
,用符号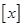 表示不超过
表示不超过 的最大整数。函数
的最大整数。函数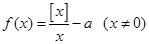 有且仅有3个零点,则
有且仅有3个零点,则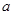 的取值范围是__________.
的取值范围是__________.
【答案】
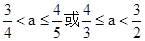
【解析】
试题分析:因为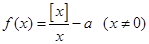 ,所以
,所以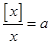 ;
;
分x>0和x<0的情况讨论,显然有a≥0.。
若x>0,此时[x]≥0;
若[x]=0,则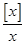 =0;
=0;
若[x]≥1,因为[x]≤x<[x]+1,故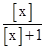 <
<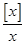 ≤1,即
≤1,即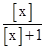 <a≤1。
<a≤1。
且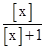 随着[x]的增大而增大。
随着[x]的增大而增大。
若x<0,此时[x]<0;
若-1≤x<0,则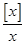 ≥1;
≥1;
若x<-1,因为[x]≤x<-1;[x]≤x<[x]+1,故1≤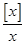 <
<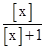 ,即1≤a<
,即1≤a<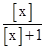 ,
,
且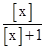 随着[x]的减小而增大。
随着[x]的减小而增大。
又因为[x]一定是,不同的x对应不同的a值。
所以为使函数f(x)= 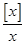 -a有且仅有3个零点,只能使[x]=1,2,3;或[x]=-1,-2,-3。
-a有且仅有3个零点,只能使[x]=1,2,3;或[x]=-1,-2,-3。
若[x]=1,有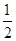 <a≤1;
<a≤1;
若[x]=2,有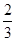 <a≤1;
<a≤1;
若[x]=3,有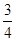 <a≤1;
<a≤1;
若[x]=4,有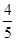 <a≤1;
<a≤1;
若[x]=-1,有a>1;
若[x]=-2,有1≤a<2;
若[x]=-3,有1≤a<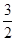 ;
;
若[x]=-4,有1≤a<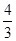 ;综上所述,
;综上所述,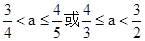
考点:本题主要考查取整函数的概念,分类讨论思想,函数的单调性,零点的概念。
点评:难题,本题考查知识点较多,难度较大,解答问题的关键是理解“取整函数”的意义,灵活运用所学知识解题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,符号
,符号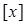 表示不超过
表示不超过 的最大整数,若关于
的最大整数,若关于 (
(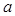 为常数)有且仅有3个不等的实根,则
为常数)有且仅有3个不等的实根,则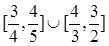 B.
B. 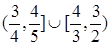
 D.
D.
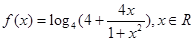 ,定义
,定义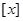 表示不超过
表示不超过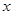 的最大整数,则函数
的最大整数,则函数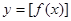 的值域是
.
的值域是
. ,符号
,符号 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数 有且仅有3个零点,则
有且仅有3个零点,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 ,符号
,符号 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数 有且仅有3个零点,则
有且仅有3个零点,则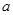 的取值范围是( )
的取值范围是( )


