题目内容
(“选修4-2矩阵与变换”)
已知y=f(x)的图象(如图1)经A=
作用后变换为曲线C(如图2).
(Ⅰ)求矩阵A;
(Ⅱ)求矩阵A的特征值.
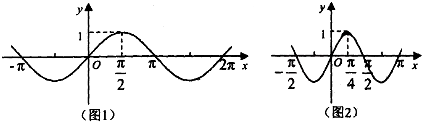
已知y=f(x)的图象(如图1)经A=
|
(Ⅰ)求矩阵A;
(Ⅱ)求矩阵A的特征值.

分析:(Ⅰ)由于y=f(x)的图象上的点(π,0)变换后为(
,0),点(
,1)变换后为(
,1),根据矩阵变换特点,写出两对坐标之间的关系,解出方程,即可得到矩阵.
(Ⅱ)先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值.
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
(Ⅱ)先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值.
解答:解:(Ⅰ) 由于y=f(x)的图象上的点(π,0)经A=
作用后变换为(
,0),
∴
=
解得 a=
,c=0,
由于y=f(x)的图象上的点(
,1)经A=
作用后变换为为(
,1),
∴
=
解得 b=0,d=1,
∴A=
;
(Ⅱ)由题意得
=0
∴(λ-
)(λ-1)=0,
解得λ=
或λ=1
∴矩阵A的特征值是
与1.
|
| π |
| 2 |
∴
|
|
|
| 1 |
| 2 |
由于y=f(x)的图象上的点(
| π |
| 2 |
|
| π |
| 4 |
∴
|
|
|
∴A=
|
(Ⅱ)由题意得
|
∴(λ-
| 1 |
| 2 |
解得λ=
| 1 |
| 2 |
∴矩阵A的特征值是
| 1 |
| 2 |
点评:本题主要考查了特征值与特征向量的计算,属于基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目