题目内容
已知数列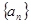 的通项公式
的通项公式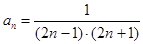 .若数列
.若数列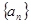 的前
的前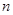 项和
项和 ,则
,则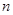 等于
等于
| A.6 | B.7 | C.8 | D.9 |
B
解析试题分析:因为数列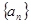 的通项公式
的通项公式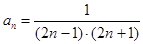 ,那么要求解数列的前n项和问题,主要是分析通项公式的特点因为
,那么要求解数列的前n项和问题,主要是分析通项公式的特点因为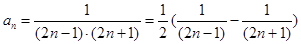 ,因此可知
,因此可知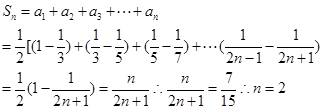
故可知n的值为7,选B.
考点:本试题主要考查了数列的前n项和的裂项法的运用问题。
点评:解决该试题的关键是对于通项公式要准确裂项表示,并求解。

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知数列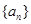 的前n项和
的前n项和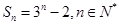 ,则( )
,则( )
A.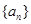 是递增的等比数列 是递增的等比数列 | B.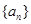 是递增数列,但不是等比数列 是递增数列,但不是等比数列 |
C.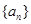 是递减的等比数列 是递减的等比数列 | D.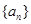 不是等比数列,也不单调 不是等比数列,也不单调 |
化简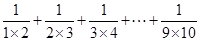 得( )
得( )
A.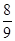 | B.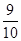 | C.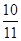 | D.1 |
已知数列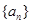 中,
中,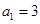 ,
,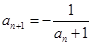 (
(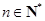 ),能使
),能使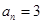 的
的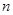 可以等于( ).
可以等于( ).
A.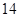 | B.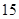 | C.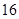 | D.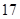 |
数列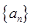 的通项公式是
的通项公式是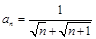 ,若前
,若前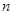 项和为
项和为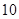 ,则项数
,则项数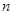 为( )
为( )
| A.120 | B.99 | C.11 | D.121 |
已知函数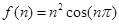 ,且
,且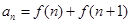 ,则
,则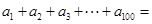 ( )
( )
| A.0 | B.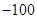 | C.100 | D.10200 |
 表示位于从上到下第
表示位于从上到下第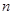 行,从左到右
行,从左到右 列的数 ,比如
列的数 ,比如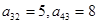 ,若
,若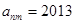 ,则有( )
,则有( )
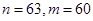
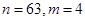
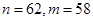

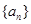 的通项公式
的通项公式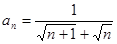 ,它的前n项和为
,它的前n项和为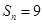 ,则
,则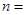 _________.
_________.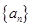 中,若
中,若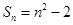 ,
,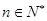 ,则
,则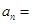 .
.