题目内容
已知tanx>0,且sinx+cosx>0,求角x的集合.
角x的集合是{x|2kπ<x<2kπ+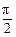 ,k∈Z}
,k∈Z}
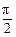 ,k∈Z}
,k∈Z} ∵tanx>0,∴x在第一或第三象限.
若x在第一象限,则sinx>0,cosx>0,∴sinx+cosx>0.
若x在第三象限,则sinx<0,cosx<0,与sinx+cosx>0矛盾,故x只能在第一象限.
因此角x的集合是{x|2kπ<x<2kπ+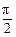 ,k∈Z}.
,k∈Z}.
若x在第一象限,则sinx>0,cosx>0,∴sinx+cosx>0.
若x在第三象限,则sinx<0,cosx<0,与sinx+cosx>0矛盾,故x只能在第一象限.
因此角x的集合是{x|2kπ<x<2kπ+
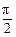 ,k∈Z}.
,k∈Z}.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为第二象限角,那么
为第二象限角,那么 ,
, ,
, ,
, 中,其值必为正的有( ).
中,其值必为正的有( ). 个
个 个
个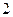 个
个 个
个 为第三象限角,试判断
为第三象限角,试判断 的符号.
的符号. 的角},N={第一象限的角},则
的角},N={第一象限的角},则 =( )
=( ) 的值是 。
的值是 。 的值等于( )
的值等于( ) 



 的终边经过点
的终边经过点 ,则
,则 的值为____________.
的值为____________.