题目内容
函数f(x)=|2x+1|+|ax|,若存在三个互不相等的实数x1,x2,x3,使得f(x1)=f(x2)=f(x3),则实数a=________.
±2
分析:题干错误:f(X3),应该为f(x3),请给修改,谢谢.
由题意可得显然a=0不满足条件,当a>0时,化简函数f(x)的解析式,画出函数的图象,数形结合可得a的值.
当a<0时,同理求得a=-2.综合可得结论.
解答:∵函数f(x)=|2x+1|+|ax|,显然a=0不满足条件.
当a>0时,f(x)=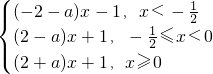 ,
,
函数的图象如图所示:其中,A(- ,
, ),B(0,1).
),B(0,1).

要使存在三个互不相等的实数x1,x2,x3,使得f(x1)=f(x2)=f(X3),必须有 ,∴a=2.
,∴a=2.
当a<0时,同理求得a=-2,故有a=±2,
故答案为±2.
点评:本题主要考查分段函数的应用,体现了数形结合和等价转化的数学思想,属于中档题.
分析:题干错误:f(X3),应该为f(x3),请给修改,谢谢.
由题意可得显然a=0不满足条件,当a>0时,化简函数f(x)的解析式,画出函数的图象,数形结合可得a的值.
当a<0时,同理求得a=-2.综合可得结论.
解答:∵函数f(x)=|2x+1|+|ax|,显然a=0不满足条件.
当a>0时,f(x)=
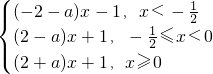 ,
,函数的图象如图所示:其中,A(-
 ,
, ),B(0,1).
),B(0,1).
要使存在三个互不相等的实数x1,x2,x3,使得f(x1)=f(x2)=f(X3),必须有
 ,∴a=2.
,∴a=2.当a<0时,同理求得a=-2,故有a=±2,
故答案为±2.
点评:本题主要考查分段函数的应用,体现了数形结合和等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
设函数f(x)=
,则满足f(x)=4的x的值是( )
|
| A、2 | B、16 |
| C、2或16 | D、-2或16 |