题目内容
已知三角形的三边构成等比数列,它们的公比为q,则q的取值范围是( )
分析:依题意,设三角形的三边分别为a,aq,aq2,利用任意两边之和大于第三边即可求得q的取值范围.
解答:解:依题意,设三角形的三边分别为a,aq,aq2,
则
,
解①得:
<q<
;④
解②得:q∈R;⑤
解③得:q>
或q<-
;⑥
由④⑤⑥得:
<q<
.
故选:D.
则
|
解①得:
1-
| ||
| 2 |
1+
| ||
| 2 |
解②得:q∈R;⑤
解③得:q>
-1+
| ||
| 2 |
1+
| ||
| 2 |
由④⑤⑥得:
-1+
| ||
| 2 |
1+
| ||
| 2 |
故选:D.
点评:本题考查等比数列的性质,考查解不等式组的能力,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
已知三角形的三边构成等比数列,且它们的公比为q,则q的取值范围是( )
A、(0,
| ||||||||
B、(
| ||||||||
C、[1,
| ||||||||
D、(
|
 ,则
,则 B.
B. C.
C. D.
D.
 ,则
,则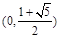 B.
B. C.
C. D.
D.
 ,则
,则 B.
B. C.
C.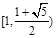 D.
D.