题目内容
(2011•顺义区一模)下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数为( )
分析:由f(x)=x-1=
是奇函数,故排除A. 由f(x)=cosx 在(0,+∞)上没有单调性,故排除B. 由f(x)=log2|x|在区间(0,+∞)上是单调递增的函数,故排除D.
经检验只有C满足条件.
| 1 |
| x |
经检验只有C满足条件.
解答:解:由于函数f(x)=x-1=
是奇函数,故排除A.
由于函数f(x)=cosx 在(0,+∞)上没有单调性,故排除B.
由于函数f(x)=(
)|x| 是偶函数,在区间(0,+∞)上f(x)=(
)x 单调递减,故C满足条件.
由于函数 f(x)=log2|x|在区间(0,+∞)上是单调递增的函数,故排除D.
故选C.
| 1 |
| x |
由于函数f(x)=cosx 在(0,+∞)上没有单调性,故排除B.
由于函数f(x)=(
| 1 |
| 2 |
| 1 |
| 2 |
由于函数 f(x)=log2|x|在区间(0,+∞)上是单调递增的函数,故排除D.
故选C.
点评:本题主要考查函数的奇偶性、单调性的判断,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
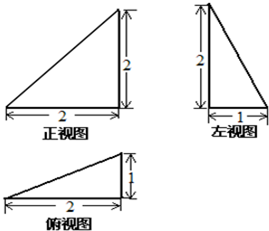 (2011•顺义区一模)一个几何体的三视图如图所示,则其表面积等于( )
(2011•顺义区一模)一个几何体的三视图如图所示,则其表面积等于( )