题目内容
已知数列 前
前 项和
项和 满足
满足 ,等差数列
,等差数列 满足
满足
(1)求数列
 的通项公式
的通项公式
(2)设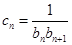 ,数列
,数列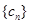 的前
的前 项和为
项和为 ,问
,问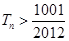 的最小正整数n是多少?
的最小正整数n是多少?
【答案】
(1)an=2n-1,bn=2n-1(2)101
【解析】
试题分析:(1)当n=1时,a1=S1=2a1-1,∴a1=1.
当n≥2时,an=Sn-Sn-1=(2an-1)-(2an-1-1)=2an-2an-1,即=2. ……2分
∴数列{an}是以a1=1为首项,2为公比的等比数列.
∴an=2n-1,Sn=2n-1. ……3分
设{bn}的公差为d,b1=a1=1,b4=1+3d=7,∴d=2.
∴bn=1+(n-1)×2=2n-1. ……6分
(2)∵cn===,
∴Tn=
==. ……10分
由Tn>,得>,解得n>100.1.
∴Tn>的最小正整数n是101. ……12分
考点:本小题主要考查等比的判断和等差、等比数列的通项公式的求解,裂项法求数列是前n项和,考查学生的运算求解能力.
点评:判断等差或等比数列时,一是用定义,一是用通项,不论用哪种方法,都不要忘记验证n=1能否适合公式.

练习册系列答案
相关题目
 前
前 项和
项和 .数列
.数列 满足
满足
 ,数列
,数列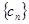 满足
满足 。
。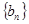 的通项公式;
的通项公式;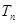 ;
; 对一切正整数
对一切正整数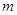 的取值范围。
的取值范围。 前
前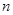 项和
项和 .数列
.数列 满足
满足
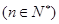 ,数列
,数列 满足
满足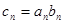 。(1)求数列
。(1)求数列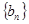 的通项公式;(2)求数列
的通项公式;(2)求数列 ;(3)若
;(3)若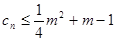 对一切正整数
对一切正整数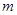 的取值范围。
的取值范围。 前
前 项和
项和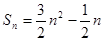 .数列
.数列 满足
满足
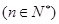 ,数列
,数列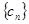 满足
满足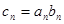 。
。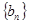 的通项公式;
的通项公式;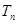 ;
;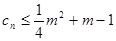 对一切正整数
对一切正整数 的取值范围。
的取值范围。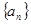 前
前 项和
项和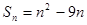 ,
, ;(2)若它的第
;(2)若它的第 项满足
项满足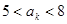 ,求
,求