题目内容
已知非零向量a,b,c满足a+b+c=0,向量a与b的夹角为60°,且|a|=|b|=1,则向量a与c的夹角为________.
150°
因为a+b+c=0,所以c=-(a+b).所以|c|2=(a+b)2=a2+b2+2a·b=2+2cos 60°=3.所以|c|=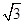 .
.
又c·a=-(a+b)·a=-a2-a·b=-1-cos 60°= -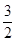 ,设向量c与a的夹角为θ,则cos θ=
,设向量c与a的夹角为θ,则cos θ= .又0°≤θ≤180°,所以θ=150°.
.又0°≤θ≤180°,所以θ=150°.
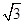 .
.又c·a=-(a+b)·a=-a2-a·b=-1-cos 60°= -
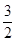 ,设向量c与a的夹角为θ,则cos θ=
,设向量c与a的夹角为θ,则cos θ= .又0°≤θ≤180°,所以θ=150°.
.又0°≤θ≤180°,所以θ=150°.
练习册系列答案
相关题目
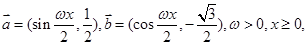 函数
函数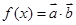 的第
的第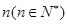 个零点记作
个零点记作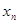 (从小到大依次计数),所有
(从小到大依次计数),所有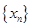 .
.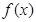 的值域;
的值域; 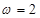 ,求数列
,求数列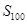 .
.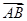 在向量
在向量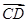 上的投影为______.
上的投影为______.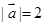 ,
,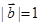 ,若
,若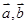 的夹角为
的夹角为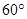 ,则
,则 .
.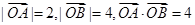 则以
则以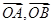 为邻边的平行四边形的面积为( )
为邻边的平行四边形的面积为( )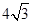
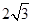
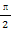 )在一个周期内的图象如图所示,M,N分别是这段图象的最高点和最低点,且
)在一个周期内的图象如图所示,M,N分别是这段图象的最高点和最低点,且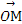 ·
·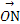 =0(O为坐标原点),则A等于( )
=0(O为坐标原点),则A等于( )
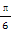
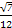 π
π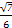 π
π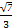 π
π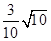
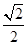
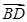 =
=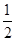
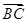 ,则
,则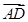 ·
·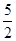
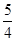
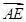 ·
·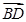 = .
= .