题目内容
已知函数f(x)=|2x-1|,a<b<c,且f(a)>f(c)>f(b),则下列结论中,一定成立的是________.
①a<0,b<0,c<0; ②a<0,b≥0,c>0;③2-a<2c; ④2a+2c<2.
①a<0,b<0,c<0; ②a<0,b≥0,c>0;③2-a<2c; ④2a+2c<2.
④
由图示可知a<0时,b的符号不确定,1>c>0,故①②错;
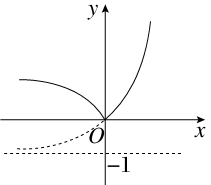
∵f(a)=|2a-1|,f(c)=|2c-1|,
∴|2a-1|>|2c-1|,
即1-2a>2c-1,
故2a+2c<2,④成立.
又2a+2c>2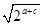 ,∴2a+c<1,
,∴2a+c<1,
∴a+c<0,∴-a>c,
∴2-a>2c,③不成立.

∵f(a)=|2a-1|,f(c)=|2c-1|,
∴|2a-1|>|2c-1|,
即1-2a>2c-1,
故2a+2c<2,④成立.
又2a+2c>2
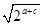 ,∴2a+c<1,
,∴2a+c<1,∴a+c<0,∴-a>c,
∴2-a>2c,③不成立.

练习册系列答案
相关题目

 a为常数且a>0.
a为常数且a>0. 对称;
对称;



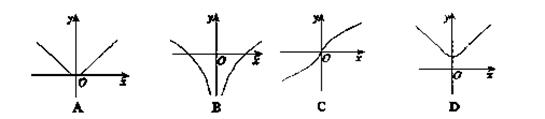
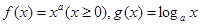 的图像可能是( )
的图像可能是( )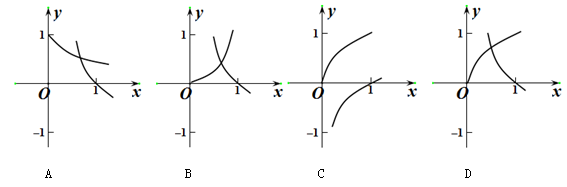
 +sinx的图象大致是( )
+sinx的图象大致是( )
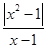 的图像与函数y=kx-2的图像恰有两个交点,则实数k的取值范围是________.
的图像与函数y=kx-2的图像恰有两个交点,则实数k的取值范围是________. =0,则y关于x的函数图象的大致形状是( )
=0,则y关于x的函数图象的大致形状是( )
 的解集是区间
的解集是区间 的子集,则实数
的子集,则实数 的取值范围是
的取值范围是