题目内容
已知函数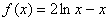 .
.
(Ⅰ)写出函数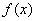 的定义域,并求其单调区间;
的定义域,并求其单调区间;
(Ⅱ)已知曲线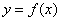 在点
在点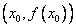 处的切线是
处的切线是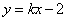 ,求
,求 的值.
的值.
【答案】
解:(Ⅰ)函数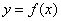 的定义域为:
的定义域为: . (1分)
. (1分)
∵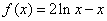 ,
,
∴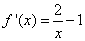 .
.
令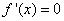 ,则
,则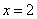 .( 3分)
.( 3分)
当 在
在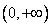 上变化时,
上变化时,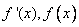 的变化情况如下表
的变化情况如下表
|
|
|
|
|
|
|
+ |
0 |
- |
|
|
↗ |
极大值 |
↘ |
(注:每对一个格给1分 )
∴函数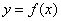 的单调递增区间是
的单调递增区间是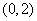 ,单调递减区间是
,单调递减区间是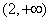 . (6分)
. (6分)
(Ⅱ)由题意可知: 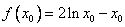 ,(7分)
,(7分)
曲线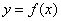 在点
在点 处的切线的斜率为
处的切线的斜率为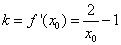 .
.
∴切线方程为: 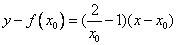 . (9分)
. (9分)
∴ .
.
∴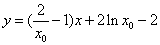 . (10分)
. (10分)
由题意知,切线方程为 ,
,
∴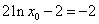 .
.
∴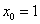 .
.
∴曲线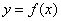 在点
在点 处的切线的斜率
处的切线的斜率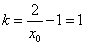 . (12分)
. (12分)
(注:若解法不同,可参考此解法相应给分)。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

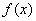
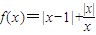 .
.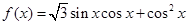 .
.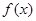 的最小正周期和单调增区间;
的最小正周期和单调增区间;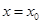 对称,且
对称,且 ,求
,求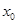 的值.
的值.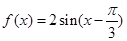 ,
,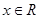 .
.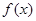 的周期;
的周期;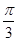 个单位,得到函数
个单位,得到函数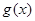 的图象,写出函数
的图象,写出函数