题目内容

5．设z=3x+5y，其中变量x和y满足条件$\left\{{\begin{array}{l}{5x+3y≤15}\\{y≤x+1{\;}^{\;}}\\{x-5y≤3}\end{array}}\right.$，求z的最大值和最小值．

分析 由约束条件作出可行域，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案

解答 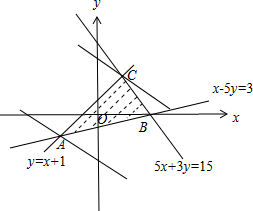解：由约束条件$\left\{{\begin{array}{l}{5x+3y≤15}\\{y≤x+1{\;}^{\;}}\\{x-5y≤3}\end{array}}\right.$，得可行域   …（6分）
交点坐标A（-2，-1），…（7分）
由z=3x+5y得$y=-\frac{3}{5}x+\frac{z}{5}$…8
当x=-2，y=-1时，zmin=-11，
当$x=\frac{3}{2}，y=\frac{5}{2}$时，zmax=17…（10分）

点评 本题考查线性规划的解得应用，考查计算能力，是中档题．

练习册系列答案
相关题目
15．设函数f（x）=Asin（ωx+φ），x∈R（其中A＞0，ω＞0），在（$\frac{π}{6}$，$\frac{π}{2}$）上既无最大值，也无最小值，且-f（$\frac{π}{2}$）=f（0）=f（$\frac{π}{6}$），则下列结论成立的是①②④．（把你认为正确结论的序号都写上）
①若f（x1）≤f（x2）对任意实数x恒成立，则x2-x1必定是$\frac{π}{2}$的整数倍；
②y=f（x）的图象关于（$\frac{4π}{3}$，0）对称；
③对于函数y=|f（x）|（x∈R）的图象，x=-$\frac{5π}{12}$一定是一条对称轴且相邻两条对称轴之间的距离是$\frac{π}{2}$；
④函数f（x）在每一个[kπ+$\frac{π}{12}$，kπ+$\frac{7π}{12}$]（k∈Z）上具有严格的单调性．
16．已知抛物线C1：y2=2px（p＞0）的焦点为F，圆C2：x2+y2=4，若C1与C2交于A，B两点，且|AB|=2$\sqrt{3}$，则抛物线C1上的点P（m，3$\sqrt{3}$）到F的距离为（　　）
A．$\frac{21}{2}$B．21C．$\frac{39}{2}$D．$\frac{39}{4}$
13．设P为直线l1：x-2y+4=0与直线l：2x-y-4=0的交点，圆C：x2+y2-4x-4y+7=0，l0为过点P且斜率为k的直线，
（1）若k=$\frac{3}{2}$，l0与圆C交于A，B两点，求|AB|；
（2）k为何值时，l0与圆C相切？设切点分别为M，N，求cos∠MPN．
20．福州为了迎接青运会，计划从2011年到2015年，每年年初投入资金用于更新和改进体育场所与设施，若2011年年初投入a万元，以后每年年初投入的资金比上一年递增10%，则投入的总资金约为（参考数据 1.14≈1.46，1.15≈1.61）（　　）
A．4.6a万元B．6.1a万元C．14.6a万元D．16.1a万元
10．比较大小：2$\sqrt{5}$＞$\sqrt{3}$+$\sqrt{7}$．
17．sin 20°cos10°+cos20°sin170°=（　　）
A．-$\frac{\sqrt{3}}{2}$B．$\frac{\sqrt{3}}{2}$C．-$\frac{1}{2}$D．$\frac{1}{2}$
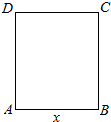14．在△ABC中，点D在边CB的延长线上，且$\overrightarrow{CD}$=4$\overrightarrow{BD}$=r$\overrightarrow{AB}$-s$\overrightarrow{AC}$，r，s∈R，求s+r的值．
15．某开心农场要用一段长为40m的篱笆，围成一个矩形菜园ABCD，若设菜园的边长AB为xm，菜园的面积为ym2．
（1）求y与x之间的函数关系式，写出x的取值范围；
（2）当x为何值时，菜园面积最大？并求出最大值？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网