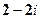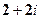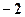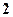题目内容
求同时满足下列条件的所有复数z:(1)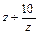 是实数,且
是实数,且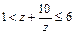 。
。
(2)z的实部和虚部都是整数。
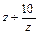 是实数,且
是实数,且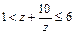 。
。(2)z的实部和虚部都是整数。
复数z为:1±3i或3±i.
设z=a+bi (a,b∈R,且a2+b2≠0).
则

由(1)知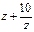 是实数,且
是实数,且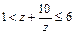 ,
,
∴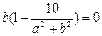 即b=0或a2+b2=10.
即b=0或a2+b2=10.
又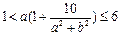 *
*
当b=0时,*化为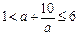 无解。
无解。
当a2+b2=10时,*化为1<2a≤6, ∴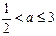 .
.
由(2)知 a=1,2,3.
∴ 相应的b=±3, ± (舍),±1,
(舍),±1,
因此,复数z为:1±3i或3±i.
此题不仅考查了复数的概念、运算等,同时也考查到了方程、不等式的解法。
则


由(1)知
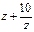 是实数,且
是实数,且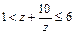 ,
,∴
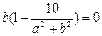 即b=0或a2+b2=10.
即b=0或a2+b2=10.又
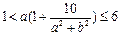 *
*当b=0时,*化为
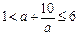 无解。
无解。当a2+b2=10时,*化为1<2a≤6, ∴
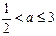 .
.由(2)知 a=1,2,3.
∴ 相应的b=±3, ±
 (舍),±1,
(舍),±1,因此,复数z为:1±3i或3±i.
此题不仅考查了复数的概念、运算等,同时也考查到了方程、不等式的解法。

练习册系列答案
相关题目
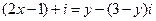 ,求x与y.
,求x与y.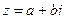 和复平面的点Z(
和复平面的点Z(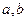 )对应,
)对应,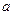 、
、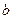 必须满足什么条件,才能使点Z位于:(1)实轴上?(2)虚轴上?(3)上半平面(含实轴)?(4)左半平面(不含虚轴及原点)?
必须满足什么条件,才能使点Z位于:(1)实轴上?(2)虚轴上?(3)上半平面(含实轴)?(4)左半平面(不含虚轴及原点)?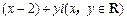 的模为
的模为 ,求
,求 的最大值.
的最大值.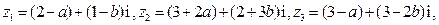 其中
其中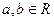 ,当
,当 取得最小值时,
取得最小值时,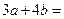 __________.
__________. ,
, ,且
,且 ,则
,则 的值为 ;
的值为 ; 的实部和虚部相等,则实数
的实部和虚部相等,则实数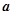 等于( )
等于( )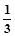
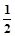
 的值等于 ( )
的值等于 ( )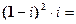 ( ).
( ).