题目内容
18.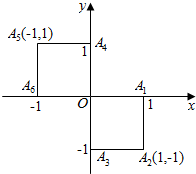 小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则:从A1,A2,A3,A4,A5,A6(如图所示)这6个点中任取两点,记选取y轴上的点(A3,A4)的个数为X,若X=0就参加学校合唱团,否则就参加排球队.
小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则:从A1,A2,A3,A4,A5,A6(如图所示)这6个点中任取两点,记选取y轴上的点(A3,A4)的个数为X,若X=0就参加学校合唱团,否则就参加排球队.(1)记“从从A1,A2,A3,A4,A5,A6中任取两点”为事件N,请列举事件N的所有可能情况;
(2)求小波不参加学校合唱团的概率.
分析 (1)记“从A1,A2,A3,A4,A5,A6中任取两点”为事件N,利用列举法能求出事件N的所有可能情况.
(2)由小波不参加学校合唱团,得选取y轴上的点(A3,A4)的个数为X,且X≠0,利用列举法求出其包含的基本事件个数,由此能求出小波不参加学校合唱团的概率.
解答 解:(1)记“从A1,A2,A3,A4,A5,A6中任取两点”为事件N,
则事件N的所有可能情况有${C}_{6}^{2}$=15个,分别为:
(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A1,A6),
(A2,A3),(A2,A4),(A2,A5),(A2,A6),(A3,A4),
(A3,A5),(A3,A6),(A4,A5),(A4,A6),(A5,A6).
(2)∵小波不参加学校合唱团,
∴选取y轴上的点(A3,A4)的个数为X,且X≠0,
包含的基本事件有:(A1,A3),(A1,A4),(A2,A3),(A2,A4),
(A3,A4),(A3,A5),(A3,A6),(A4,A5),(A4,A6),共9个,
∴小波不参加学校合唱团的概率p=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
6.已知抛物线y2=4x的焦点为F,过点(a,0)(a<0)倾斜角为$\frac{π}{6}$的直线l交抛物线C、D两点.若F在以线段CD为直径的圆的外部,则a的取值范围为( )
| A. | (-3,-2$\sqrt{5}$+3) | B. | (-∞,-2$\sqrt{5}$+3) | C. | (-$\frac{1}{2}$,4-$\sqrt{17}$) | D. | (-∞,4-$\sqrt{17}$) |
10. 如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )
如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )
 如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )
如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )| A. | [0,$\frac{\sqrt{2}}{8}$]∪($\frac{5\sqrt{2}}{8}$,1) | B. | [$\frac{\sqrt{2}}{8}$,$\frac{5\sqrt{2}}{8}$] | C. | [0,$\frac{\sqrt{2}}{8}$] | D. | [0,$\frac{5\sqrt{2}}{8}$] |