题目内容
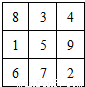
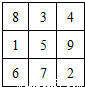
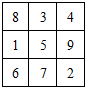 将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如右图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于( )
将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如右图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于( )| A、44 | B、42 | C、40 | D、36 |
分析:根据题意可知,幻方对角线上的数成等差数列,根据等差数列的性质可知对角上的两个数相加正好等于1+n2,进而根据等差数列的求和公式求得答案.
解答:解:依题意每行.每列.每条对角线上数的和都相等,而4×4方格中填入的各数成等差数列,总和为16×3+
=168,
所以每行上数的和为168/4=42,从而每条对角线上的数的和为42.
故选B.
| 16×15×1 |
| 2 |
所以每行上数的和为168/4=42,从而每条对角线上的数的和为42.
故选B.
点评:本题主要考查了等差数列的性质,幻方的题很有趣味性,它的幻和的公式可记住,便于以后解此类的问题.

练习册系列答案
相关题目
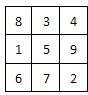 将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于
将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于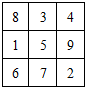 将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如右图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于
将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如右图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于