题目内容
已知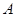
、
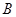两个盒子中分别装有标记为
，
，
，
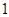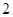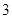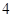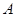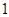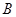的大小相同的四个小球，甲从盒中等可能地取出个球，乙从盒中等可能地取出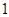个球．
（1）用有序数对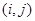
表示事件“甲抽到标号为i的小球，乙抽到标号为是j的小球”，求取出的两球标号之和为5的概率；
（2）甲、乙两人玩游戏，约定规则：若甲抽到的小球的标号比乙大，则甲胜；反之，则乙胜．你认为此规则是否公平？请说明理由．
【答案】
（1）取出的两球标号之和为5的概率为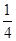
. （2）此游戏不公平．
【解析】（I）用列举法一一列举出甲、乙二人抽到的小球的所有情况，共16种不同情况．
（Ⅱ）．甲抽到的小球的标号比乙大，有共6种情况；故甲胜的概率p1=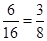
，乙获胜的概率为p2=
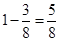，故此游戏不公平．
（1）设“取出的两球标号之和为5”为事件M，则甲、乙二人抽到的小球的所有情况有：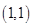
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
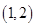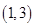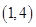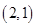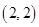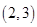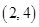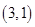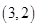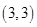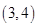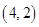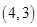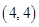，共16种不同情况，且每种情况均等可能出现，又事件M 包含的情况有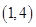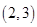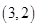：、、、，共4种情况，由古典概型概率公式有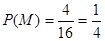
.
答：取出的两球标号之和为5的概率为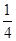. ……6分
（2）甲抽到的小球的标号比乙大，有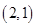、、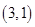、、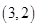、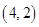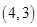，共6种情况，故甲胜的概率
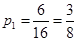，又事件甲胜与事件乙胜是对立事件，所以乙获胜的概率为
．因为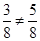
，所以此游戏不公平．
……12分
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目