题目内容
下列函数是奇函数的是 ( )
A.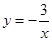 | B. | C. | D. |
A
解析试题分析:奇函数的定义域关于原点对称,并且还满足f(-x)=-f(x).据此可知只有A满足此要求.
考点:函数的图像及奇偶性.
点评:判断函数的奇偶性应先判断定义域是否关于原点对称,然后再判断f(-x)=f(x)是偶函数,f(-x)=-f(x)是奇函数.否则是非奇非偶函数.易错点:忘记判断定义域是否关于原点对称造成错误.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
函数 的定义域是( )
的定义域是( )
A.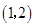 | B.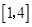 | C. | D. |
已知函数 ,则
,则 的值为( )
的值为( )
A. | B. | C.0 | D.-1 |
已知函数 是偶函数,当
是偶函数,当 时,
时, 恒成立,设
恒成立,设 ,则
,则 的大小关系为( )
的大小关系为( )
A. | B.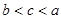 | C. | D. |
函数 的图象如图所示,其中
的图象如图所示,其中 为常数,则下列结论正确的是
为常数,则下列结论正确的是
A. | B. | C. | D. |
函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. | C. | D. |
下列各组函数中表示同一函数的是( )
A. | B. |
C.f(x)=( )2,g(x)= )2,g(x)= | D. |
 与
与 的图象是 ( )
的图象是 ( )
 的图象是( )
的图象是( )