题目内容
如果曲线y=x3+x-10的某一切线与直线y=4x+3平行,求切点坐标与切线方程.
【答案】分析:利用直线平行斜率相等求出切线的斜率,再利用导数在切点处的值是曲线的切线斜率求出切线斜率,列出方程解得.
解答:解:∵切线与直线y=4x+3平行,斜率为4
又切线在点x的斜率为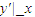
∵3x2+1=4,∴x=±1,有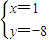 ,或
,或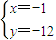 ,
,
∴切点为(1,-8)或(-1,-12),
切线方程为y+8=4(x-1)或y+12=4(x-1),
即y=4x-12或y=4x-8.
点评:本题考查导数的几何意义:导数在切点处的值是切线的斜率.
解答:解:∵切线与直线y=4x+3平行,斜率为4
又切线在点x的斜率为
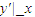
∵3x2+1=4,∴x=±1,有
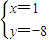 ,或
,或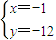 ,
,∴切点为(1,-8)或(-1,-12),
切线方程为y+8=4(x-1)或y+12=4(x-1),
即y=4x-12或y=4x-8.
点评:本题考查导数的几何意义:导数在切点处的值是切线的斜率.

练习册系列答案
相关题目