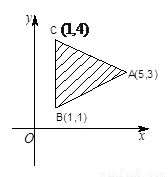题目内容
 已知平面区域如图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m=
已知平面区域如图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m=| 7 |
| 20 |
| 7 |
| 20 |
分析:目标函数Z=mx+y,取得最大值的最优解有无数个知取得最优解必在边界上,目标函数的截距取得最大值,故最大值应在左上方边界AC上取到,即mx+y=0应与直线AC平行;进而计算可得m的值.
解答:解:由题意,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,
最优解应在线段AC上取到,故mx+y=0应与直线AC平行
∵kAC=
=-
,
∴-m=-
,
∴m=
,
故答案为:
.

最优解应在线段AC上取到,故mx+y=0应与直线AC平行
∵kAC=
| ||
| 1-5 |
| 7 |
| 20 |
∴-m=-
| 7 |
| 20 |
∴m=
| 7 |
| 20 |
故答案为:
| 7 |
| 20 |
点评:目标函数的最优解有无数多个,处理方法一般是:①将目标函数的解析式进行变形,化成斜截式②分析Z与截距的关系,是符号相同,还是相反③根据分析结果,结合图形做出结论④根据斜率相等求出参数.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
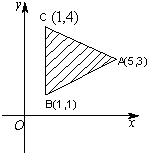 已知平面区域如图所示,z=x+my(m>0)在平面区域内取得最大值时的解(x,y)有无数多个,则m=
已知平面区域如图所示,z=x+my(m>0)在平面区域内取得最大值时的解(x,y)有无数多个,则m=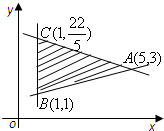 已知平面区域如图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m的值为( )
已知平面区域如图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m的值为( )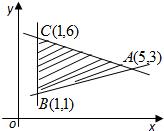 已知平面区域如图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m的值为( )
已知平面区域如图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m的值为( ) 在平面区域内取得最大值时的解
在平面区域内取得最大值时的解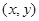 有无数多个,则
有无数多个,则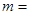 ★ .
★ .