题目内容
(本小题满分12分)
已知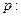 关于
关于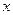 的不等式
的不等式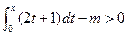 对任意
对任意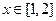 恒成立;
恒成立;
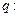
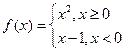 ,不等式
,不等式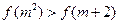 成立。
成立。
若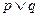 为真,
为真,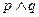 为假,求
为假,求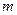 的取值范围。
的取值范围。
已知
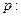 关于
关于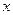 的不等式
的不等式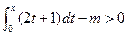 对任意
对任意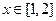 恒成立;
恒成立;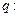
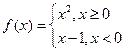 ,不等式
,不等式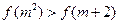 成立。
成立。若
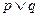 为真,
为真,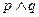 为假,求
为假,求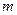 的取值范围。
的取值范围。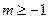 且
且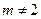 。
。解:关于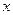 的不等式
的不等式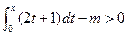 对任意
对任意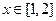 恒成立,即
恒成立,即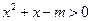 在
在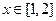 上恒成立。由于
上恒成立。由于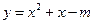 在
在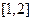 上是增函数,所以
上是增函数,所以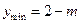 ,要保证
,要保证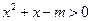 在
在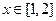 上恒成立,只要
上恒成立,只要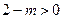 即可,所以
即可,所以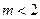 。
。
因为 在
在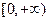 上是增函数,
上是增函数,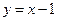 在
在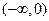 上也是增函数,且
上也是增函数,且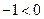 ,所以
,所以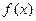 在
在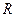 上是增函数,因此不等式
上是增函数,因此不等式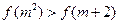 等价于
等价于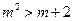 ,所以
,所以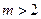 或
或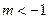 。
。
若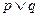 为真,
为真,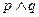 为假,所以
为假,所以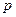 与
与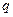 一真一假,
一真一假,
若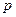 真
真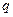 假,应有
假,应有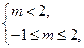 所以
所以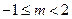 ;
;
若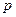 假
假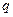 真,应有
真,应有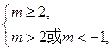 所以
所以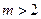 ;
;
因此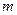 的范围是
的范围是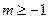 且
且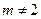 。
。
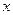 的不等式
的不等式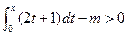 对任意
对任意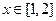 恒成立,即
恒成立,即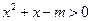 在
在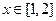 上恒成立。由于
上恒成立。由于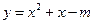 在
在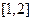 上是增函数,所以
上是增函数,所以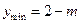 ,要保证
,要保证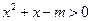 在
在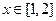 上恒成立,只要
上恒成立,只要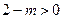 即可,所以
即可,所以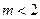 。
。因为
 在
在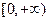 上是增函数,
上是增函数,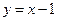 在
在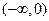 上也是增函数,且
上也是增函数,且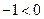 ,所以
,所以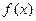 在
在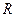 上是增函数,因此不等式
上是增函数,因此不等式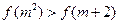 等价于
等价于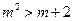 ,所以
,所以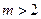 或
或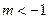 。
。若
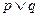 为真,
为真,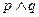 为假,所以
为假,所以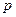 与
与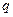 一真一假,
一真一假,若
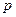 真
真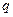 假,应有
假,应有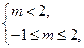 所以
所以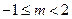 ;
;若
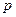 假
假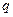 真,应有
真,应有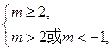 所以
所以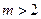 ;
;因此
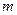 的范围是
的范围是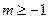 且
且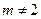 。
。
练习册系列答案
相关题目
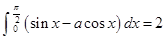 ,则实数
,则实数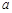 等于( )
等于( )



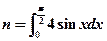 ,则
,则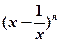 展开式中的常数项为
展开式中的常数项为 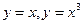 围成的封闭图形面积为( )[
围成的封闭图形面积为( )[



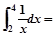 ( )。
( )。



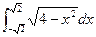 =________________。
=________________。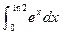 的值为( ).
的值为( ).



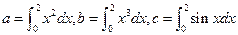 ,则
,则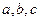 大小关系是 ( )
大小关系是 ( )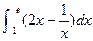 的值是( )
的值是( )


