题目内容
为了保护三峡库区的生态环境,凡是坡度在25°以上的坡荒地都要绿化造林,经初步统计,在三峡库区内坡度大于25°的坡荒地面积约有2640万亩,若从2003年初开始绿化造林,第一年造林120万亩,以后每年比前一年多绿化60万亩.(1)若所有被绿化造林的坡荒地全都成功,问到哪一年底可使库区的坡荒地全部绿化?
(2)若每万亩绿化造林所植树苗的木材量平均为0.1万立方米,每年树木木材量的自然生长率为20%,那么当整个库区25°以上坡荒地全部绿化完成的那一年底,一共有木材多少万立方米?(保留1位小数,1.29=5.16,1.28=4.30)
【答案】分析:(1)由于从2003年初开始绿化造林,第一年造林120万亩,以后每年比前一年多绿化60万亩,设每年应绿化的坡荒地面积为an则{an}为等差数列,从而可求前n项的和,要使库区的坡荒地全部绿化,则有Sn≥2640,从而问题可解.
(2)设该库区每年拥有木材量为bn,则有b1=120×0.1×(1+20%)8=12×1.28;b2=(120+60)×0.1×(1+20%)7=18×1.27;…b8=(120+60×7)×(1+20%)=54×1.2,∴S8=b1+b2+…+b8=6(2×1.28+3×1.27+…+9×1.2),利用错位相减法可求.
解答:解:(1)设每年应绿化的坡荒地面积为an(单位:万亩),则{an}为等差数列.
∵a1=120,d=60,∴Sn=120n+ ×n(n-1)×60
×n(n-1)×60
令Sn≥2640,即4n+n(n-1)≥88,(n+11)(n-8)≥0,n∈N+,∴n≥8.
故到第8年底,即2010年底可使库区的坡荒地全部绿化.…(5分)
(2)设该库区每年拥有木材量为bn(含种植的树苗及自然生长量,单位:万m3).则
b1=120×0.1×(1+20%)8=12×1.28;
b2=(120+60)×0.1×(1+20%)7=18×1.27;
…
b8=(120+60×7)×(1+20%)=54×1.2,
∴S8=b1+b2+…+b8=6(2×1.28+3×1.27+…+9×1.2)(1)…8分
1.2S8=6(2×1.29+3×1.28+…+9×1.22) (2)
由(2)-(1)得 0.2 S8=6(2×1.29+1.28+1.27+…1.22-9×1.2)
∴S8=30[2×1.29+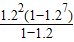 -9×1.2]=30[2×1.29+5(1.29-1.22)-9×1.2]=30(7×5.16-5×1.44-9×1.2)
-9×1.2]=30[2×1.29+5(1.29-1.22)-9×1.2]=30(7×5.16-5×1.44-9×1.2)
=30(36.12-18)=543.6.
故到2010年底共有木材543.6万m3.…(13分)
点评:本题主要考查数列模型的简历,考查错位相减法求和,有一定的综合性.
(2)设该库区每年拥有木材量为bn,则有b1=120×0.1×(1+20%)8=12×1.28;b2=(120+60)×0.1×(1+20%)7=18×1.27;…b8=(120+60×7)×(1+20%)=54×1.2,∴S8=b1+b2+…+b8=6(2×1.28+3×1.27+…+9×1.2),利用错位相减法可求.
解答:解:(1)设每年应绿化的坡荒地面积为an(单位:万亩),则{an}为等差数列.
∵a1=120,d=60,∴Sn=120n+
 ×n(n-1)×60
×n(n-1)×60令Sn≥2640,即4n+n(n-1)≥88,(n+11)(n-8)≥0,n∈N+,∴n≥8.
故到第8年底,即2010年底可使库区的坡荒地全部绿化.…(5分)
(2)设该库区每年拥有木材量为bn(含种植的树苗及自然生长量,单位:万m3).则
b1=120×0.1×(1+20%)8=12×1.28;
b2=(120+60)×0.1×(1+20%)7=18×1.27;
…
b8=(120+60×7)×(1+20%)=54×1.2,
∴S8=b1+b2+…+b8=6(2×1.28+3×1.27+…+9×1.2)(1)…8分
1.2S8=6(2×1.29+3×1.28+…+9×1.22) (2)
由(2)-(1)得 0.2 S8=6(2×1.29+1.28+1.27+…1.22-9×1.2)
∴S8=30[2×1.29+
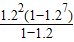 -9×1.2]=30[2×1.29+5(1.29-1.22)-9×1.2]=30(7×5.16-5×1.44-9×1.2)
-9×1.2]=30[2×1.29+5(1.29-1.22)-9×1.2]=30(7×5.16-5×1.44-9×1.2)=30(36.12-18)=543.6.
故到2010年底共有木材543.6万m3.…(13分)
点评:本题主要考查数列模型的简历,考查错位相减法求和,有一定的综合性.

练习册系列答案
相关题目
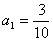 ,经过一年绿化面积为a2,…,经过n年绿化面积为
,经过一年绿化面积为a2,…,经过n年绿化面积为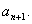
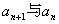 的关系式,并证明数列
的关系式,并证明数列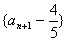 是等比数列;
是等比数列;