题目内容
A.(坐标系与参数方程)已知直线的参数方程为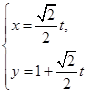 (为参数),圆
(为参数),圆 的参数方程为
的参数方程为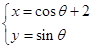 (
(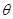 为参数), 则圆心
为参数), 则圆心 到直线的距离为_________.
到直线的距离为_________.
B.(几何证明选讲)如右图,直线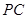 与圆
与圆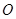 相切于点
相切于点 ,割线
,割线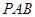 经过圆心
经过圆心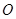 ,弦
,弦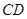 ⊥
⊥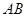 于点
于点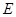 ,
, 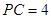 ,
,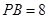 ,则
,则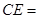 _________.
_________.
C.(不等式选讲)若存在实数 使
使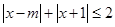 成立,则实数
成立,则实数
的取值范围是_________.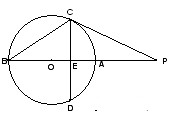
A. 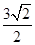 ; B.
; B.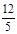 ; C.
; C.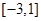
解析试题分析:A. 先把直线l和圆C的参数方程化为普通方程y=x+1,(x-2)2+y2=1,再利用点到直线的距离公式求出即可.
B.在圆中线段利用由切割线定理求得PA,进而利用直角三角形PCO中的线段,结合面积法求得CE即可.
C. 由绝对值的基本不等式得: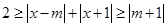 ,解得-3≤m≤1.
,解得-3≤m≤1.
考点:(1)参数方程;(2)圆的性质;(3)绝对值不等式.

练习册系列答案
相关题目
不等式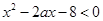 对于一切
对于一切 都成立,则x的范围是
都成立,则x的范围是
A. | B.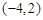 | C. | D. |
 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围为 .
的取值范围为 . 的不等式
的不等式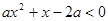 的解集中有且仅有4个整数解,则实数
的解集中有且仅有4个整数解,则实数 的取值范围是 .
的取值范围是 . 的不等式
的不等式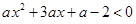 的解集为
的解集为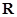 ,则实数
,则实数 的取值范围 .
的取值范围 .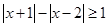 解集是_____________________.
解集是_____________________. 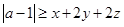 对满足
对满足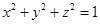 的一切实数
的一切实数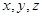 恒成立,则
恒成立,则 的取值范围是_________.
的取值范围是_________.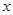 使
使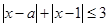 成立,则实数
成立,则实数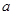 的取值范围_______
的取值范围_______