题目内容
某工厂日生产某种产品最多不超过30件,且在生产过程中次品率p与日产量x(x∈N+)件间的关系为p=
|
(Ⅰ)将日利润y(元)表示为日产量x(件)的函数;
(Ⅱ)该厂的日产量为多少件时,日利润最大?
(注:次品率p=
| 次品个数 |
| 产品总数 |
分析:(I)由已知中,工厂日生产某种产品最多不超过30件,且在生产过程中次品率p与日产量x(x∈N+)件间的关系为,p=
,每生产一件正品盈利2900元,每出现一件次品亏损1100元.我们易得到日利润y(元)表示为日产量x(件)的分段函数的形式,
(II)根据分段函数分段处理的原则,我们求出两段的最大值,进而分析两个最大值,即可得到结论.
|
(II)根据分段函数分段处理的原则,我们求出两段的最大值,进而分析两个最大值,即可得到结论.
解答:解:(Ⅰ)由题意得:
y=
=
(6分)
(II)当0<x≤15时,y=2500x-20x2,
∴当x=15时,y取得最大值33000元…6分
当15<x≤30时,y=2500x-
x3
则y′=2500-4x2,令y′=0,则x=25
∵当15<x≤25时,y′≥0,当25<x≤30,y′<0…8分
故当x=25时,y取得最大值
元…10分
∵33000<
∴当x=25时,y取得最大值
元
即该厂的日产量为25件时,日利润最大…12分
y=
|
=
|
(II)当0<x≤15时,y=2500x-20x2,
∴当x=15时,y取得最大值33000元…6分
当15<x≤30时,y=2500x-
| 4 |
| 3 |
则y′=2500-4x2,令y′=0,则x=25
∵当15<x≤25时,y′≥0,当25<x≤30,y′<0…8分
故当x=25时,y取得最大值
| 125000 |
| 3 |
∵33000<
| 125000 |
| 3 |
∴当x=25时,y取得最大值
| 125000 |
| 3 |
即该厂的日产量为25件时,日利润最大…12分
点评:本题考查的知识点是函数模型的选择与应用,利用导数求半月区间上的函数的最值,其中分析题意,求出满足条件的函数的解析式,是解答本题的关键.

练习册系列答案
相关题目
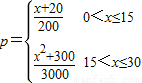 ,每生产一件正品盈利2900元,每出现一件次品亏损1100元.
,每生产一件正品盈利2900元,每出现一件次品亏损1100元. ,正品率=1-p)
,正品率=1-p)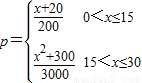 ,每生产一件正品盈利2900元,每出现一件次品亏损1100元.
,每生产一件正品盈利2900元,每出现一件次品亏损1100元. ,正品率=1-p)
,正品率=1-p)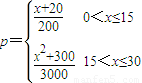 ,每生产一件正品盈利2900元,每出现一件次品亏损1100元.
,每生产一件正品盈利2900元,每出现一件次品亏损1100元. ,正品率=1-p)
,正品率=1-p) 与日产量
与日产量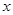 (
(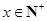 )件间的关系为
)件间的关系为
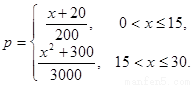 ,每生产一件正品盈利2900元,每出现一件次品亏损1100元.
,每生产一件正品盈利2900元,每出现一件次品亏损1100元.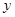 (元)表示为日产量
(元)表示为日产量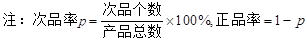 )
)