题目内容
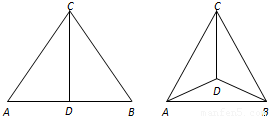
如图,一个等腰直角三角形的硬纸片△ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高,沿CD把△ABC折成直二面角.
 ⑴如果你手中只有一把能够量长度的直尺,应该如何确定A、B的位置,使得二面角A—CD—B是直二面角?证明你的结论.
⑴如果你手中只有一把能够量长度的直尺,应该如何确定A、B的位置,使得二面角A—CD—B是直二面角?证明你的结论.
⑵试在平面ABC上确定一点P,使DP与平面ABC内任意一条直线垂直,证明你的结论.
⑶如果在折成的三棱锥内有一个小球,求出球的半径的最大值.
(本题满分14分)
解:⑴用直尺度量折后的AB长,若AB=4cm,则二面角A-CD-B是直二面角
∵△ABC是等腰直角三角形,∴AD=DB=![]()
又∵AD⊥DC,BD⊥DC,∴∠ADC为二面角A-CD-B的平面角 4分
⑵取△ABC的中心P,连DP,则DP满足条件
∵△ABC此时为正三角形,且AD=DB=DC
∵三棱锥D-ABC是正三棱锥,由P为△ABC的中心知DP⊥面ABC
∴DP与平面ABC内任意一条直线垂直 8分
(3)当小球半径最大时,此时小球与三棱锥的四个面都相切
设该小球的球心为O,半径为r,连结OA,OB,OC,OD
三棱锥被分成了四个小三棱锥,且每个小三棱锥中有一个面上的高都为r
故有![]() 代入得即小球的半径最大
代入得即小球的半径最大
值为![]() 14分
14分

练习册系列答案
相关题目
 如图,一个等腰直角三角形的硬纸片△ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高,沿CD把△ABC折成直二面角.
如图,一个等腰直角三角形的硬纸片△ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高,沿CD把△ABC折成直二面角. (2013•广州二模)如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为 圆心,l为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P,则点P落在区 域M内的概率为
(2013•广州二模)如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为 圆心,l为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P,则点P落在区 域M内的概率为 (图中白色部分).若在此三角形内随机取一点
(图中白色部分).若在此三角形内随机取一点 ,则点
,则点