题目内容
设a>0,b>0,2c>a+b.
求证:(1) >ab;(2)c-
>ab;(2)c- <a<c+
<a<c+ .
.
答案:
解析:
解析:
|
证 (1)∵a>0,b>0,∴2c>a+b≥ (2)要证原不等式成立,只要证 说明 利用|a-c|< |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
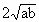 ,∴c>
,∴c>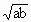 >0,∴
>0,∴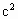 >ab.
>ab.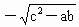 <a-c<
<a-c<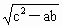
 |a-c|<
|a-c|<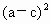 <
<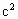 -ab,而
-ab,而 +ab,∴
+ab,∴ C. 4 D.
C. 4 D.
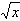 ,g(x)=alnx,a∈R。
,g(x)=alnx,a∈R。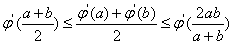 。
。