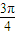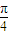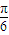题目内容
已知向量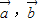 满足
满足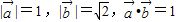 ,则
,则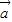 与
与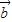 的夹角为( )
的夹角为( )A.
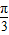
B.
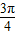
C.
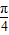
D.
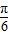
【答案】分析:设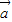 与
与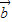 的夹角为θ,由向量数量积的公式列出关于θ的等式,可解出cosθ的值,再结合θ的范围,可得
的夹角为θ,由向量数量积的公式列出关于θ的等式,可解出cosθ的值,再结合θ的范围,可得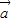 与
与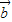 的夹角θ的值.
的夹角θ的值.
解答:解:∵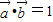
∴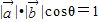 ,其中θ为
,其中θ为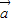 与
与 的夹角
的夹角
又∵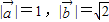
∴1×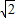 cosθ=1,解得cosθ=
cosθ=1,解得cosθ=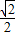
∵θ∈(0,π)
∴θ=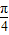
故选C
点评:本题在已知向量的模和数量积的情况下,求向量的夹角,考查了平面向量数量积的定义、夹角范围等知识,属于基础题.
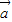 与
与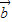 的夹角为θ,由向量数量积的公式列出关于θ的等式,可解出cosθ的值,再结合θ的范围,可得
的夹角为θ,由向量数量积的公式列出关于θ的等式,可解出cosθ的值,再结合θ的范围,可得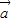 与
与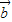 的夹角θ的值.
的夹角θ的值.解答:解:∵
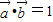
∴
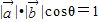 ,其中θ为
,其中θ为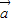 与
与 的夹角
的夹角又∵
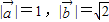
∴1×
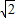 cosθ=1,解得cosθ=
cosθ=1,解得cosθ=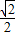
∵θ∈(0,π)
∴θ=
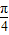
故选C
点评:本题在已知向量的模和数量积的情况下,求向量的夹角,考查了平面向量数量积的定义、夹角范围等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 满足
满足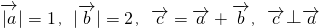 ,则
,则 与
与 的夹角等于
的夹角等于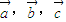 满足
满足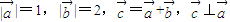 ,则
,则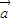 与
与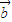 的夹角等于( )
的夹角等于( )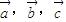 满足
满足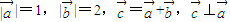 ,则
,则 与
与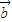 的夹角等于( )
的夹角等于( )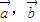 满足
满足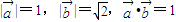 ,则
,则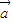 与
与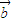 的夹角为( )
的夹角为( )