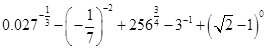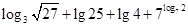题目内容
已知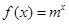 (m为常数,m>0且m≠1).
(m为常数,m>0且m≠1).
设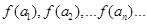 (n∈
(n∈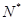 ?)是首项为m2,公比为m的等比数列.
?)是首项为m2,公比为m的等比数列.
(1)求证:数列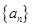 是等差数列;
是等差数列;
(2)若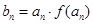 ,且数列
,且数列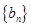 的前n项和为Sn,当m=2时,求Sn;
的前n项和为Sn,当m=2时,求Sn;
(3)若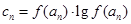 ,问是否存在m,使得数列
,问是否存在m,使得数列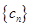 中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由.
中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由.
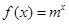 (m为常数,m>0且m≠1).
(m为常数,m>0且m≠1).设
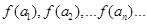 (n∈
(n∈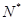 ?)是首项为m2,公比为m的等比数列.
?)是首项为m2,公比为m的等比数列.(1)求证:数列
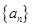 是等差数列;
是等差数列; (2)若
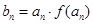 ,且数列
,且数列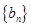 的前n项和为Sn,当m=2时,求Sn;
的前n项和为Sn,当m=2时,求Sn;(3)若
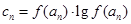 ,问是否存在m,使得数列
,问是否存在m,使得数列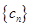 中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由.
中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由..解:(1)由题意f(an)=
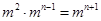 ,即
,即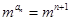 .
.∴an=n+1,(2分) ∴an+1-an=1,
∴数列{an}是以2为首项,1为公差的等差数列.(4分)
(2)由题意
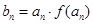 =(n+1)·mn+1,
=(n+1)·mn+1,当m=2时,bn=(n+1)·2n+1
∴Sn=2·22+3·23+4·24+…+(n+1)·2n+1 ①(6分)
①式两端同乘以2,得
2Sn=2·23+3·24+4·25+…+n·2n+1+(n+1)·2n+2 ②
②-①并整理,得
Sn=-2·22-23-24-25-…-2n+1+(n+1)·2n+2
=-22-(22+23+24+…+2n+1)+(n+1)·2n+2
=-22-+(n+1)·2n+2
=-22+22(1-2n)+(n+1)·2n+2=2n+2·n.(9分)
(3)由题意
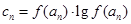 =mn+1·lgmn+1=(n+1)·mn+1·lgm,
=mn+1·lgmn+1=(n+1)·mn+1·lgm,要使cn<cn+1对一切n∈N*成立,
即(n+1)·mn+1·lgm<(n+2)·mn+2·lgm,对一切n∈N*成立,
①当m>1时,lgm>0,所以n+1<m(n+2)对一切n∈N*恒成立;
(11分)
②当0<m<1时,lgm<0,所以等价使得>m对一切n∈N*成立,
因为=1-的最小值为,所以0<m<.
综上,当0<m<或m>1时,数列{cn}中每一项恒小于它后面的项.
(14分)
略

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
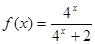 ,若
,若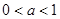 ,试求:
,试求: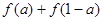 的值;
的值;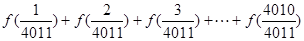 的值;
的值;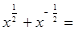 3,求
3,求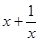 的值;
的值; 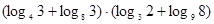

 的值域是
的值域是



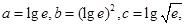 则( )
则( )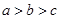
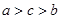
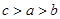
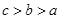
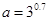 .
.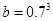 .
.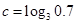 的大小顺序为( )
的大小顺序为( )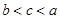
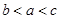
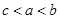
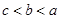
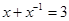 ,则
,则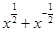 值为( )
值为( )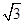
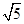
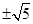
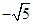
 上的函数
上的函数 满足
满足 ,又
,又 ,
, ,
,