题目内容
如图，一个水平放置的平面图的斜二测直观图是一个底角为45°、腰和上底长为1的等腰梯形，试画出这个平面图形并求它的面积．
【答案】分析：依据题意，画出试画出这个平面图形，根据题意，利用余弦定理求出直角梯形ABCD，底边的长，求出高，然后求出面积．
解答：
解：作辅助线D′E′，
利用余弦定理12=12+|E′C′|2-2|E′C′|cos45°．
可得|E′C′|=
，
从而在图（2）直角梯形ABCD中，AD=1，BC=1+
，AB=2，其面积为2+
．
所求面积为2+
．
点评：本题考查平面图形的直观图，余弦定理，考查作图能力，计算能力，是基础题．
解答：
解：作辅助线D′E′，利用余弦定理12=12+|E′C′|2-2|E′C′|cos45°．
可得|E′C′|=
，从而在图（2）直角梯形ABCD中，AD=1，BC=1+
，AB=2，其面积为2+．所求面积为2+
．点评：本题考查平面图形的直观图，余弦定理，考查作图能力，计算能力，是基础题．
练习册系列答案
相关题目
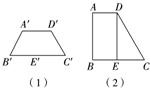如图，一个水平放置的平面图的斜二测直观图是一个底角为45°、腰和上底长为1的等腰梯形，试画出这个平面图形并求它的面积．
如图，一个水平放置的三角形的斜二侧直观图是等腰直角三角形A′B′O′，若O′A′=2，那么原三角形ABO的最长边的长度为（ ）
B．
C．
D．2
B． 
C． 
D． 
是一个水平放置的正三棱柱
，
是棱
的中点．正三棱柱的主视图如图
．
的平面有哪几个？（直接写出符合要求的平面即可，不必说明或证明）
.